Neste tópico
Etapa1: Determine se as diferenças entre as médias do grupo são estatisticamente significativas
- Valor-p ≤ α: as diferenças entre algumas das médias são estatisticamente significativas
- Se o valor-p for menor ou igual ao nível de significância, rejeite a hipótese nula e conclua que nem todas as médias da população são iguais. Use seu conhecimento especializado para determinar se as diferenças são significativas na prática. Para obter mais informações, acesse Significância prática e estatística.
- Valor-p > α: as diferenças entre algumas das médias não são estatisticamente significativas
- Se o valor-p for maior do que o nível de significância, não há provas suficientes para rejeitar a hipótese nula de que as médias da população são todos iguais. Certifique-se de que o teste tenha poder suficiente para detectar uma diferença que seja significativa na prática. Para obter mais informações, vá para Aumentar o poder de um teste de hipóteses.
Análise de Variância
| Fonte | GL | SQ (Aj.) | QM (Aj.) | Valor F | Valor-P |
|---|---|---|---|---|---|
| Paint | 3 | 281,7 | 93,90 | 6,02 | 0,004 |
| Erro | 20 | 312,1 | 15,60 | ||
| Total | 23 | 593,8 |
Resultados principais: valor-p
Nestes resultados, a hipótese nula afirma que os valores médios de dureza de 4 tintas diferentes são iguais. Como o valor de p é menor que o nível de significância de 0,05, é possível rejeitar a hipótese nula e concluir que algumas das tintas têm médias diferentes.
Etapa 2: Examine as médias do grupo
Utilize o gráfico de intervalo para exibir a média e o intervalo de confiança para cada grupo.
- Cada ponto representa uma média da amostra.
- Cada intervalo é um intervalo de confiança de 95% para a média de um grupo. É possível ter 95% de confiança de que a média do grupo está dentro do intervalo de confiança do grupo.
Importante
Interprete esses intervalos com cuidado, pois fazer comparações múltiplas aumenta a taxa de erro tipo 1. Ou seja, quando você aumenta o número de comparações, também aumenta a probabilidade de que pelo menos uma comparação conclua incorretamente que uma das diferenças observadas seja significativamente diferente.
Para avaliar as diferenças que aparecem neste gráfico, use a tabela de informações de agrupamento e a outra de saída de comparações (mostrada na etapa 3).
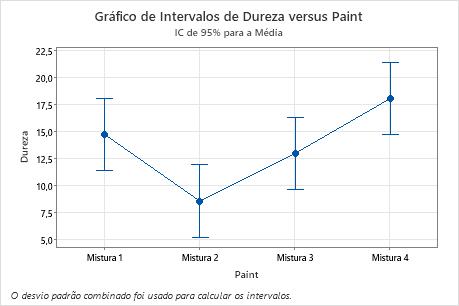
No gráfico de intervalo, a Mistura 2 tem a menor média e a Mistura 4 tem a maior. Não é possível determinar, a partir desse gráfico, se qualquer diferença é estatisticamente significativa. Para determinar a significância estatística, avalie os intervalos de confiança para as diferenças das médias.
Etapa 3: Compare as médias de grupo
Se o valor de p da ANOVA com um fator for menor do que o nível de significância, saiba que algumas das médias do grupo são diferentes, mas não quaisquer pares de grupos. Use a tabela de informações de agrupamento e testes de diferenças de médias para determinar se a diferença média entre pares específicos de grupos são estatisticamente significativas e estime por quanto elas são diferentes.
Para mais informações sobre métodos de comparação, acesse Utilizando várias comparações para avaliar a significância prática e estatística.
- Tabela de informações de agrupamento
-
Use a tabela de informações de agrupamento para determinar rapidamente se a diferença média entre qualquer par de grupos é estatisticamente significativa.
Grupos que têm a mesma letra são significativamente diferentes.
- Testes para diferenças de médias
-
Use os intervalos de confiança para determinar os intervalos prováveis para as diferenças e para determinar se as diferenças são significativas na prática. A tabela exibe um conjunto de intervalos de confiança para a diferença entre pares de médias. O gráfico de intervalo para as diferenças de médias mostra as mesmas informações.
Os intervalos de confiança que não contêm zero indicam uma diferença média que é estatisticamente significativa.
Dependendo do método de comparação escolhido, a tabela compara pares de grupos diferentes e exibe um dos seguintes tipos de intervalos de confiança.-
Nível de confiança individual
A porcentagem de vezes que um único intervalo de confiança inclui a verdadeira diferença entre um par de médias de grupo, se você repetir o estudo várias vezes.
-
Nível de confiança simultâneo
A porcentagem de vezes que um conjunto de intervalos de confiança inclui as diferenças verdadeiras para todas as comparações entre os grupos, se você repetir o estudo várias vezes.
Controlar o nível de confiança simultâneo é particularmente importante quando você realiza várias comparações. Se você não controlar o nível de confiança simultâneo, a chance de que, pelo menos um intervalo de confiança não contenha a diferença verdadeira, aumenta com o número de comparações.
-
Para obter mais informações, acesse Compreendendo os níveis de confiança individuais e simultâneos em múltiplas comparações.
Para obter mais informações sobre como interpretar os resultados para o método MCB de Hsu, acesse O que é múltiplas comparações com o melhor de Hsu (MCB)?
Informações de Agrupamento Usando Método de Tukey e 95% de Confiança
| Paint | N | Média | Agrupamento | |
|---|---|---|---|---|
| Mistura 4 | 6 | 18,07 | A | |
| Mistura 1 | 6 | 14,73 | A | B |
| Mistura 3 | 6 | 12,98 | A | B |
| Mistura 2 | 6 | 8,57 | B | |
Principais resultados: Média, Agrupamento
Nestes resultados, o quadro mostra que o grupo A contém as Misturas de 1, 3 e 4, e o grupo B contém as Misturas de 1, 2 e 3. As Misturas 1 e 3 estão em ambos os grupos. As diferenças entre as médias que compartilham uma letra não são estatisticamente significativas. As Misturas de 2 e 4 não compartilham nenhuma letra, o que indica que a Mistura 4 tem uma média significativamente mais elevada do que a Mistura 2.
Testes Simultâneos de Tukey para Diferenças de Médias
| Diferença de Níveis | Diferença de Médias | EP da Diferença | IC de 95% | Valor-T | Valor-P Ajustado |
|---|---|---|---|---|---|
| Mistura 2 - Mistura 1 | -6,17 | 2,28 | (-12,55; 0,22) | -2,70 | 0,061 |
| Mistura 3 - Mistura 1 | -1,75 | 2,28 | (-8,14; 4,64) | -0,77 | 0,868 |
| Mistura 4 - Mistura 1 | 3,33 | 2,28 | (-3,05; 9,72) | 1,46 | 0,478 |
| Mistura 3 - Mistura 2 | 4,42 | 2,28 | (-1,97; 10,80) | 1,94 | 0,245 |
| Mistura 4 - Mistura 2 | 9,50 | 2,28 | (3,11; 15,89) | 4,17 | 0,002 |
| Mistura 4 - Mistura 3 | 5,08 | 2,28 | (-1,30; 11,47) | 2,23 | 0,150 |
Principais resultados: IC de 95% simultâneo, nível de confiança individual
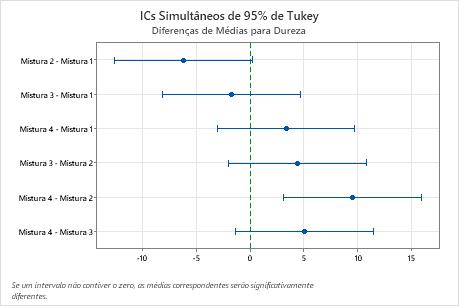
- O intervalo de confiança para a diferença entre as médias da Mistura de 2 e 4 é 3,11 a 15,89. Esta variação não inclui zero, o que indica que a diferença é estatisticamente significativa.
- Todos os intervalos de confiança para os pares de médias restantes incluem zero, o que indica que as diferenças não são estatisticamente significativas.
- O nível de confiança simultâneo de 95% indica que é possível ter 95% de confiança de que todos os intervalos de confiança de contêm as verdadeiras diferenças.
- A tabela indica que o nível de confiança individual é 98,89%. Este resultado indica que é possível ter a confiança de que 98,89% cada intervalo individual contém a verdadeira diferença entre um par específico de médias de grupo. Os níveis de confiança individuais para cada comparação produzem o nível de confiança simultâneo de 95% para todas as seis comparações.
Etapa 4: Determine se o modelo ajusta bem os dados
Para determinar se o modelo ajusta bem os dados, examine as estatísticas de qualidade do ajuste tabela do resumo do modelo.
- S
- Use S para avaliar se o modelo descreve bem a resposta.
S é medido nas unidades da variável de resposta e representa o quão longe os valores de dados caem dos valores ajustados. Quanto mais baixo for o valor de S, melhor o modelo descreve a resposta. No entanto, um valor de S baixo por si só não indica que o modelo satisfaz aos pressupostos do modelo. Você deve verificar os gráficos de resíduos para conferir os pressupostos.
- R2
-
R2 representa a porcentagem de variação na resposta que é explicada pelo modelo. Quanto mais alto o valor de R2 melhor o modelo ajusta seus dados. O valor de R2 está sempre entre 0 e 100%.
Um valor de R2 elevado não indica que o modelo satisfaz aos pressupostos do modelo. Você deve verificar os gráficos de resíduos para conferir os pressupostos.
- R2 (pred)
-
Use R2 predito para determinar o quão bem seu modelo prediz as respostas para novas observações.Modelos que têm valores de R2 predito mais elevado têm melhor capacidade preditiva.
Um R2 predito que é substancialmente menor que o R2 pode indicar que o modelo está com excesso de ajuste. Um modelo com excesso de ajuste ocorre quando você adiciona termos para efeitos que não são importantes na população. O modelo se adapta aos dados de amostra e, por conseguinte, pode não ser útil para fazer predições em relação à população.
O R2 previsto também pode ser mais útil do que o R2 ajustado para a comparação de modelos, porque ele é calculado com as observações que não estão incluídas no cálculo do modelo.
Sumário do Modelo
| S | R2 | R2(aj) | R2(pred) |
|---|---|---|---|
| 3,95012 | 47,44% | 39,56% | 24,32% |
Principais resultados: S, R2, R2 (pred)
Nestes resultados, o fator explica 47,44% da variação na resposta. S indica que o desvio padrão entre os pontos de dados e os valores ajustados é de aproximadamente 3,95 unidades.
Etapa 5: Determinar se o modelo atende às suposições da análise
Use os gráficos de resíduos para ajudar a determinar se o modelo é adequado e satisfaz aos pressupostos da análise. Se os pressupostos não forem satisfeitos, o modelo pode não ajustar bem os dados e você deve ter cautela ao interpretar os resultados.
Gráficos de resíduos versus de ajustes
Use o gráfico de resíduos versus ajustes para verificar a pressuposição de que os resíduos são aleatoriamente distribuídos e têm variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Um ponto que está distante de zero | Um outlier |
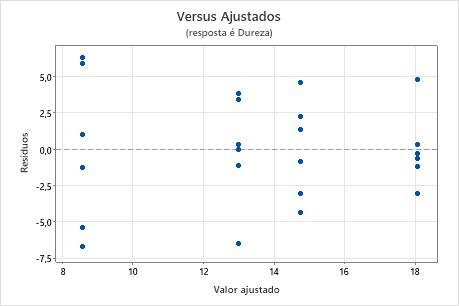
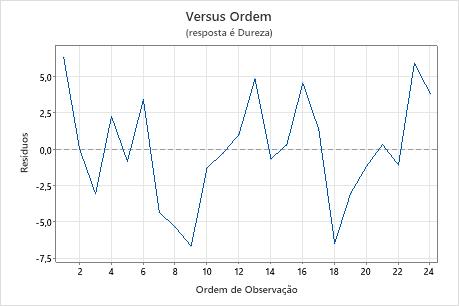
Gráfico de resíduos versus ordem
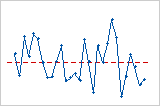
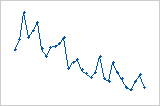
Tendência
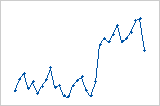
Deslocamento
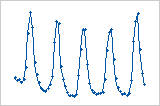
Ciclo
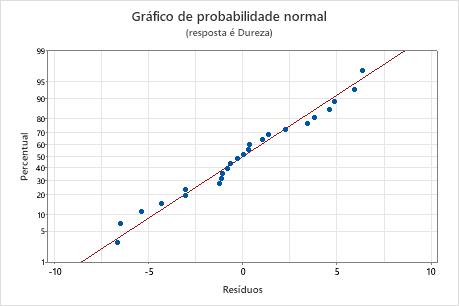
Gráficos de probabilidade normal dos resíduos
Use o gráfico de probabilidade normal de resíduos para verificar a pressuposição de que os resíduos são distribuídos normalmente. O gráfico de probabilidade normal dos resíduos deve seguir aproximadamente uma linha reta.
| Padrão | O que o padrão pode indicar |
|---|---|
| Não é uma linha reta | Não normalidade |
| Um ponto que está distante da linha | Um outlier |
| Alteração de inclinação | Uma variável não identificada |
Observação
Se seu experimento ANOVA com um fator atender às diretrizes para tamanho amostral, os resultados não são substancialmente afetados por desvios da normalidade.