Neste tópico
N
O tamanho amostral (N) é o número total de observações em cada grupo.
Interpretação
O tamanho amostral afeta o intervalo de confiança e o poder do teste.
Normalmente, uma amostra maior produz um intervalo de confiança mais estreito. Uma amostra maior também proporciona ao teste mais poder para detectar uma diferença.
Média
A média das observações dentro de cada grupo. A média descreve cada grupo com um valor único que identificando o centro dos dados. Ele é a soma de todas as observações com um grupo dividido pelo número de observações naquele grupo.
Interpretação
A média de cada amostra fornece uma estimativa de cada média da população. As diferenças entre as médias amostrais são as estimativas da diferença entre as médias da população.
Como a diferença entre as médias de grupo é baseada nos dados de uma amostra e não em toda a população, não é possível ter certeza de que ela é igual à diferença da população. Para ter uma noção melhor da diferença população, você pode usar o intervalo de confiança.
Agrupamento
Use a tabela de informações de agrupamento para determinar rapidamente se a diferença média entre qualquer par de grupos é estatisticamente significativa.
A coluna Agrupamento contém letras que agrupam os níveis de fator. Os grupos que não compartilham uma letra têm uma diferença média que é estatisticamente significativa.
Se a tabela identificar diferenças que são estatisticamente significativas, utilize os intervalos de confiança das diferenças para determinar se as diferenças são significativas na prática.
Interpretação
Informações de Agrupamento Usando Método de Tukey e 95% de Confiança
| Paint | N | Média | Agrupamento | |
|---|---|---|---|---|
| Mistura 4 | 6 | 18,07 | A | |
| Mistura 1 | 6 | 14,73 | A | B |
| Mistura 3 | 6 | 12,98 | A | B |
| Mistura 2 | 6 | 8,57 | B | |
Nestes resultados, o quadro mostra que o grupo A contém as Misturas de 1, 3 e 4, e o grupo B contém as Misturas de 1, 2 e 3. As Misturas 1 e 3 estão em ambos os grupos. As diferenças entre as médias que compartilham uma letra não são estatisticamente significativas. As Misturas de 2 e 4 não compartilham nenhuma letra, o que indica que a Mistura 4 tem uma média significativamente mais elevada do que a Mistura 2.
Testes individuais de Fisher para diferenças de médias
Use os intervalos de confiança individuais para identificar diferenças estatisticamente significativas entre as médias dos grupos, para determinar as prováveis faixas para as diferenças e para determinar se as diferenças são significativas na prática. A tabela de testes individuais de Fisher exibe um conjunto de intervalos de confiança para a diferença entre pares de médias.
O nível de confiança individual é a porcentagem de vezes que um intervalo de confiança único inclui a verdadeira diferença entre um par de médias do grupo, se você repetir o estudo. Os intervalos de confiança individuais estão disponíveis somente para o método de Fisher. Todos os outros métodos de comparação produzem os intervalos de confiança simultâneos.
Controlar o nível de confiança individual é incomum porque ele não controla o nível de confiança simultâneo, que muitas vezes aumenta para níveis inaceitáveis. Se você não controlar o nível de confiança simultâneo, a chance de que, pelo menos um intervalo de confiança não contenha a diferença verdadeira, aumenta com o número de comparações.
O intervalo de confiança da diferença é composto pelas duas partes a seguir:
- Estimativa de ponto
- A estimativa pontual é a diferença entre um par de médias, e é calculada a partir dos dados da amostra. O intervalo de confiança é centrado em torno deste valor.
- Margem de erro
- A margem de erro define a largura do intervalo de confiança e é determinada pela variabilidade observada na amostra e no nível de confiança. Para calcular o limite superior do intervalo de confiança, a margem de erro é adicionada à estimativa do ponto. Para calcular o limite inferior do intervalo de confiança, a margem de erro é subtraída da estimativa do ponto.
Interpretação
Use os intervalos de confiança para avaliar as diferenças entre médias de grupos.
Testes Individuais de Fisher para Diferenças de Médias
| Diferença de Níveis | Diferença de Médias | EP da Diferença | IC de 95% | Valor-T | Valor-P Ajustado |
|---|---|---|---|---|---|
| Mistura 2 - Mistura 1 | -6,17 | 2,28 | (-10,92; -1,41) | -2,70 | 0,014 |
| Mistura 3 - Mistura 1 | -1,75 | 2,28 | (-6,51; 3,01) | -0,77 | 0,452 |
| Mistura 4 - Mistura 1 | 3,33 | 2,28 | (-1,42; 8,09) | 1,46 | 0,159 |
| Mistura 3 - Mistura 2 | 4,42 | 2,28 | (-0,34; 9,17) | 1,94 | 0,067 |
| Mistura 4 - Mistura 2 | 9,50 | 2,28 | (4,74; 14,26) | 4,17 | 0,000 |
| Mistura 4 - Mistura 3 | 5,08 | 2,28 | (0,33; 9,84) | 2,23 | 0,037 |
- O intervalo de confiança para a diferença entre as médias da Mistura de 4 e 2 estende de 4,74 para 14,26. Esta variação não inclui zero, o que indica que a diferença entre estas médias é estatisticamente significativa.
- O intervalo de confiança para a diferença entre as médias da Mistura de 2 e 1 estende de -10,92 para -1,41. Esta variação não inclui zero, o que indica que a diferença entre estas médias é estatisticamente significativa.
- O intervalo de confiança para a diferença entre as médias da Mistura de 4 e 3 estende de 0,33 para 9,84. Esta variação não inclui zero, o que indica que a diferença entre estas médias é estatisticamente significativa.
- Todos os intervalos de confiança para os pares de médias restantes incluem zero, o que indica que as diferenças não são estatisticamente significativas.
- O nível de confiança individual de 95% indica que você pode ter 95% confiança de que cada intervalo de confiança contém a verdadeira diferença para essa comparação específica. No entanto, o nível de confiança simultânea indica que você pode ter apenas 80,83% de confiança de que todos os intervalos contenham as verdadeiras diferenças.
Diferença das médias
Este valor é a diferença entre as médias das amostras de dois grupos.
Interpretação
As diferenças entre as médias dos grupos de amostras são as estimativas das diferenças entre as populações desses grupos.
Como cada diferença média é baseada nos dados de uma amostra e não de toda a população, não é possível ter certeza de que ela seja igual à diferença população. Para entender melhor as diferenças entre as médias populacionais, use os intervalos de confiança.
SE da diferença
O erro padrão da diferença entre as médias (SE da diferença) estima a variabilidade da diferença entre as médias das amostras que poderiam ser obtidas se você extraísse repetidas amostras das mesmas populações.
Interpretação
Use o erro padrão da diferença entre as médias para determinar o quão precisamente as diferenças entre as médias de amostra estimam as diferenças entre as médias da população. Um valor menor do erro padrão indica uma estimativa mais precisa.
O Minitab usa o erro padrão da diferença para calcular os intervalos de confiança das diferenças entre as médias, que é uma variação de valores que tende a incluir as diferenças da população.
IC de 95%
Use os intervalos de confiança simultâneos da diferença (IC de 95%) para identificar diferenças médias que são estatisticamente significativas, para determinar prováveis intervalos para as diferenças e para avaliar a significância prática das diferenças. A tabela exibe um conjunto de intervalos de confiança para a diferença entre pares de médias. Os intervalos de confiança que não contêm zero indicam uma diferença média que é estatisticamente significativa.
O nível de confiança simultânea é a porcentagem de vezes que um conjunto de intervalos de confiança inclui as verdadeiras diferenças para todas as comparações entre os grupos se o estudo foi repetido várias vezes.
Controlar o nível de confiança simultâneo é particularmente importante quando você realiza várias comparações. Se você não controlar o nível de confiança simultâneo, a chance de que, pelo menos um intervalo de confiança não contenha a diferença verdadeira, aumenta com o número de comparações.
O intervalo de confiança da diferença é composto pelas duas partes a seguir:
- Estimativa de ponto
- A estimativa pontual é a diferença entre um par de médias, e é calculada a partir dos dados da amostra. O intervalo de confiança é centrado em torno deste valor.
- Margem de erro
- A margem de erro define a largura do intervalo de confiança e é determinada pela variabilidade observada na amostra, o tamanho da amostra e o nível de confiança. Para calcular o limite superior do intervalo de confiança, a margem de erro é adicionada à estimativa pontual. Para calcular o limite inferior do intervalo de confiança, a margem de erro é subtraída da estimativa pontual. A margem aumenta à medida que o número de comparações aumenta, a fim de manter o nível de confiança simultâneo de que todos os intervalos contêm as verdadeiras diferenças de população.
Interpretação
Use os intervalos de confiança para avaliar as diferenças entre médias de grupos.
Testes Simultâneos de Tukey para Diferenças de Médias
| Diferença de Níveis | Diferença de Médias | EP da Diferença | IC de 95% | Valor-T | Valor-P Ajustado |
|---|---|---|---|---|---|
| Mistura 2 - Mistura 1 | -6,17 | 2,28 | (-12,55; 0,22) | -2,70 | 0,061 |
| Mistura 3 - Mistura 1 | -1,75 | 2,28 | (-8,14; 4,64) | -0,77 | 0,868 |
| Mistura 4 - Mistura 1 | 3,33 | 2,28 | (-3,05; 9,72) | 1,46 | 0,478 |
| Mistura 3 - Mistura 2 | 4,42 | 2,28 | (-1,97; 10,80) | 1,94 | 0,245 |
| Mistura 4 - Mistura 2 | 9,50 | 2,28 | (3,11; 15,89) | 4,17 | 0,002 |
| Mistura 4 - Mistura 3 | 5,08 | 2,28 | (-1,30; 11,47) | 2,23 | 0,150 |
- O intervalo de confiança para a diferença entre as médias da Mistura de 2 e Mistura 4 estende de 3,11 para 15,89. Esta variação não inclui zero, o que indica que a diferença é estatisticamente significativa.
- Todos os intervalos de confiança para os pares de médias restantes incluem zero, o que indica que as diferenças não são estatisticamente significativas.
- O nível de confiança simultâneo de 95% indica que é possível ter 95% de confiança de que todos esses intervalos de confiança contêm as verdadeiras diferenças.
- O nível de confiança individual de 98,89% indica que é possível ter 98,89% confiança de que cada intervalo de confiança contém a verdadeira diferença para essa comparação específica.
Valor-t
O valor-t é um teste estatístico que mede a razão entre a diferença nas médias e o erro padrão da diferença.
Interpretação
É possível usar um valor de T para determinar se você deve rejeitar a hipótese nula, que afirma que a diferença nas médias é 0. No entanto, a maioria das pessoas usa o valor de p, porque é mais fácil de ser interpretado. Para obter mais informações sobre como usar o valor crítico, acesse Usando o valor-t para determinar se a hipótese nula deve ser rejeitada.
O Minitab usa o valor de T para calcular o valor de p.
Valor de p de ajustado
O valor de p ajustado indica que os pares dentro de uma família de comparações são significativamente diferentes. O ajuste limita a taxa de erro da família para o nível alfa que você especificar. Se for usado um valor de p regular para várias comparações, a taxa de erro da família aumenta com cada comparação adicional.
É importante considerar a taxa de erro de família ao efetuar múltiplas comparações, porque as chances de cometer um erro do tipo I para uma série de comparações é maior do que a taxa de erro para uma comparação separada.
Interpretação
Se o valor de p é ajustado for menor que alfa, você deve rejeitar a hipótese nula e concluir que a diferença entre um par de médias de grupo é estatisticamente significativa. O valor de p ajustado representa também a menor taxa de erro de família em que uma hipótese nula específica é rejeitada.
Gráfico de intervalos para diferenças de médias
Use os intervalos de confiança para determinar as prováveis variações para as diferenças e avalie a significância prática das diferenças. O gráfico exibe um conjunto de intervalos de confiança para a diferença entre pares de médias. Os intervalos de confiança que não contêm zero indicam uma diferença média que é estatisticamente significativa.
Dependendo do método de comparação escolhido, o gráfico compara pares de grupos diferentes e exibe um dos seguintes tipos de intervalos de confiança.
-
Nível de confiança individual
A porcentagem de vezes que um único intervalo de confiança incluiria a verdadeira diferença entre um par de médias de grupo, se o estudo fosse repetido várias vezes.
-
Nível de confiança simultâneo
A porcentagem de tempo em que um conjunto de intervalos de confiança incluiria as diferenças verdadeiras para todas as comparações de grupo, se o estudo fosse repetido múltiplas vezes.
Controlar o nível de confiança simultâneo é particularmente importante quando você realiza várias comparações. Se você não controlar o nível de confiança simultâneo, a chance de que, pelo menos um intervalo de confiança não contenha a diferença verdadeira, aumenta com o número de comparações.
Interpretação
- O intervalo de confiança para a diferença entre as médias da Mistura de 4 e Mistura 2 estende de 3,11 para 15,89. Esta variação não inclui zero, o que indica que a diferença entre estas médias é estatisticamente significativa.
- Todos os intervalos de confiança para os pares de médias restantes incluem zero, o que indica que as diferenças não são estatisticamente significativas.
- O nível de confiança simultâneo de 95% indica que é possível ter 95% de confiança de que todos esses intervalos de confiança contêm as verdadeiras diferenças.
- Cada intervalo de confiança individual tem um nível de confiança de 98,89%. Este resultado indica que é possível ter a confiança de que 98,89% cada intervalo individual contém a verdadeira diferença entre um par específico de médias de grupo. Os níveis de confiança individuais para cada comparação produzem o nível de confiança simultâneo de 95% para todas as seis comparações.
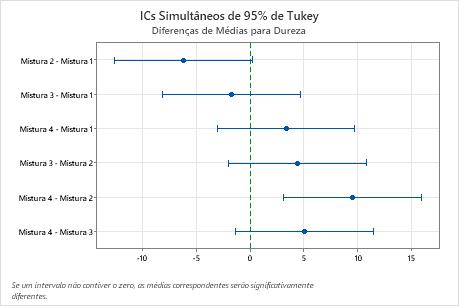
Testes Simultâneos de Tukey para Diferenças de Médias
| Diferença de Níveis | Diferença de Médias | EP da Diferença | IC de 95% | Valor-T | Valor-P Ajustado |
|---|---|---|---|---|---|
| Mistura 2 - Mistura 1 | -6,17 | 2,28 | (-12,55; 0,22) | -2,70 | 0,061 |
| Mistura 3 - Mistura 1 | -1,75 | 2,28 | (-8,14; 4,64) | -0,77 | 0,868 |
| Mistura 4 - Mistura 1 | 3,33 | 2,28 | (-3,05; 9,72) | 1,46 | 0,478 |
| Mistura 3 - Mistura 2 | 4,42 | 2,28 | (-1,97; 10,80) | 1,94 | 0,245 |
| Mistura 4 - Mistura 2 | 9,50 | 2,28 | (3,11; 15,89) | 4,17 | 0,002 |
| Mistura 4 - Mistura 3 | 5,08 | 2,28 | (-1,30; 11,47) | 2,23 | 0,150 |
