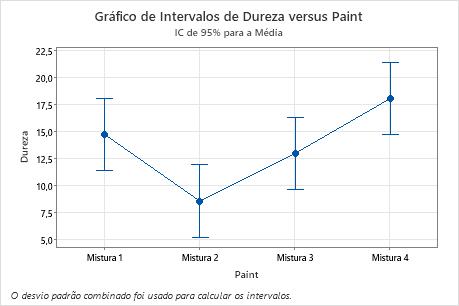
Um engenheiro químico deseja comparar a dureza de quatro misturas de tinta. Seis amostras de cada mistura de tinta foram aplicadas a uma peça de metal. As peças de metal foram curadas. Depois, a dureza de cada amostra foi medida. A fim de testar a igualdade das médias e avaliar as diferenças entre os pares de médias, o analista utiliza a ANOVA com um fator com várias comparações.
- Abra os dados das amostras, DurezaDaTinta.MWX.
- Selecione .
- Selecione Os dados de resposta estão em uma coluna para todos os níveis dos fatores.
- Em Resposta, insira Dureza.
- Em Fator, insira Paint.
- Clique no botão Comparações e, em seguida, selecione Tukey.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
O valor de p para a ANOVA da dureza da tinta é menor do que 0,05. Este resultado indica que a dureza das misturas de tinta difere significativamente. O engenheiro sabe que algumas das médias do grupo são diferentes.
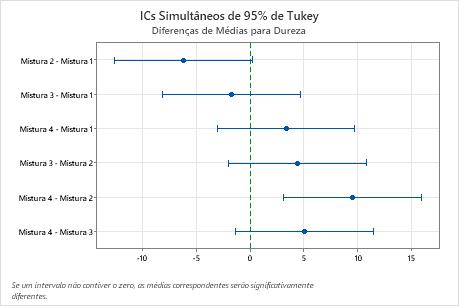
O engenheiro utiliza os resultados da comparação de Tukey para testar formalmente se a diferença entre um par de grupos é estatisticamente significativa. O gráfico que inclui os intervalos de confiança simultâneos de Tukey mostram que o intervalo de confiança para a diferença entre as médias das Misturas 2 e 4 é 3,114 a15,886. Esta variação não inclui zero, o que indica que a diferença entre estas médias é estatisticamente significativa. O engenheiro pode usar esta estimativa da diferença para determinar se a diferença tem significância prática.
Todos os intervalos de confiança para os pares de médias restantes incluem zero, o que indica que as diferenças não são significativas.
Um valor de R2 predito baixo (24,32%) indica que o modelo gera predições imprecisas para novas observações. A imprecisão pode ser devida ao tamanho pequeno dos grupos. Assim, o engenheiro não deve usar o modelo para fazer generalizações além dos dados da amostra.
Método
| Hipótese nula | Todas as médias são iguais |
|---|
| Hipótese alternativa | Nem todas as médias são iguais |
|---|
| Nível de significância | α = 0,05 |
|---|
Informações dos Fatores
| Paint | 4 | Mistura 1; Mistura 2; Mistura 3; Mistura 4 |
|---|
Análise de Variância
| Paint | 3 | 281,7 | 93,90 | 6,02 | 0,004 |
|---|
| Erro | 20 | 312,1 | 15,60 | | |
|---|
| Total | 23 | 593,8 | | | |
|---|
Sumário do Modelo
| 3,95012 | 47,44% | 39,56% | 24,32% |
Médias
| Mistura 1 | 6 | 14,73 | 3,36 | (11,37; 18,10) |
|---|
| Mistura 2 | 6 | 8,57 | 5,50 | (5,20; 11,93) |
|---|
| Mistura 3 | 6 | 12,98 | 3,73 | (9,62; 16,35) |
|---|
| Mistura 4 | 6 | 18,07 | 2,64 | (14,70; 21,43) |
|---|
Informações de Agrupamento Usando Método de Tukey e 95% de Confiança
| Mistura 4 | 6 | 18,07 | A | |
|---|
| Mistura 1 | 6 | 14,73 | A | B |
|---|
| Mistura 3 | 6 | 12,98 | A | B |
|---|
| Mistura 2 | 6 | 8,57 | | B |
|---|