Neste tópico
Componentes da variância
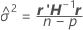
onde 

Para obter detalhes sobre a estimativa de θi, consulte [1].
Para obter mais detalhes sobre a notação, vá para a seção Métodos.
Referências
- Hemmerle, W. and Hartley, H. (1973). Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation. Technometrics, 15(4):819–831.
Erros padrão de componentes da variância
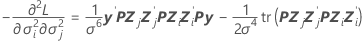
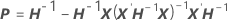
 coluna, j = 1, …, c:
coluna, j = 1, …, c:
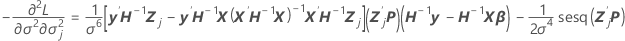

Este componente também é o valor da última coluna e a  linha pela propriedade simetria da matriz de variância-covariância.
linha pela propriedade simetria da matriz de variância-covariância.

A matriz de variância-covariância assintótica das estimativas de componentes de variância é duas vezes o inverso da matriz de informações de Fisher observada. As estimativas dos erros padrão são as raízes quadradas dos elementos diagonais da matriz de variância-covariância. Os primeiros elementos diagonais c são para os componentes de variância dos termos de efeitos aleatórios. O último elemento da diagonal é para o componente de variância de erro.
Notação
| Termo | Descrição |
|---|---|
 | o traço da matriz  |
 | a soma dos quadrados de todos os elementos na matriz M |
Para obter mais detalhes sobre a notação, vá para a seção Métodos.
Intervalos de confiança para componentes da variância
O Minitab usa o método delta para construir limites de confiança tipo Wald para o log natural dos componentes da variância, depois exponencia os intervalos de confiança para obter os intervalos de confiança para os componentes da variância. As fórmulas para os componentes de variância para erro têm a mesma forma.
Intervalo bilateral
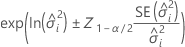
Limite inferior
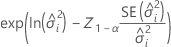
Limite superior
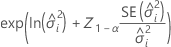
Notação
| Termo | Descrição |
|---|---|
 | o 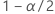 quantil da distribuição normal padrão quantil da distribuição normal padrão |
 | 1 − nível de confiança |
 | o erro padrão do  componente de variância componente de variância |
 | o componente da variância para o  termo de efeito aleatório termo de efeito aleatório |
Valor-z e valor-p
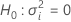
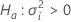


Notação
| Termo | Descrição |
|---|---|
| Z | o valor da função de distribuição acumulada para a distribuição normal padrão |
Matriz de variância-covariância
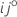 componente da matriz de informações observadas de Fisher:
componente da matriz de informações observadas de Fisher:
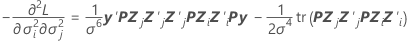

 coluna, j = 1, …, c:
coluna, j = 1, …, c:
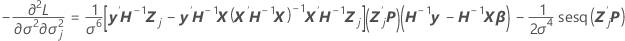

Este componente também é o valor da última coluna e a  linha pela propriedade simetria da matriz de variância-covariância.
linha pela propriedade simetria da matriz de variância-covariância.

Notação
| Termo | Descrição |
|---|---|
 | o traço da matriz  |
Para obter mais detalhes sobre a notação, vá para a seção Métodos.
