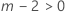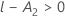Neste tópico
Testes de termos de efeitos fixos
Os testes dos termos de efeitos fixos são os testes-F. A hipótese nula para o teste depende se o teste é destinado a um termo de fator fixo ou a um termo de covariável. Para um termo de fator fixo, a hipótese nula é que o termo não afeta significativamente a resposta. Para um termo de covariável, a hipótese nula é que não existe nenhuma associação entre a resposta e o termo de covariável.
O Minitab oferece 2 métodos para testar termos de efeitos fixos: métodos de aproximação de Kenward-Roger e de aproximação Satterthwaite. Para obter mais informações sobre o método de aproximação de Kenward-Roger, consulte Kenward e Roger.1 Para obter mais informações sobre o método de aproximação de Satterthwaite, consulte Giesbrecht e Burns 2, bem como Fai e Cornelius. 3
O cálculo dos graus de liberdade do denominador para a estatística-F e o cálculo da estatística F são diferentes. O cálculo dos graus de liberdade do numerador e a determinação de um valor-p para uma determinada estatística-F são os mesmos para ambos os métodos.
Aproximação de Kenward-Roger
A aproximação de Kenward-Roger é um método para testar a significância estatística em termos de efeito fixo.
Estatística F
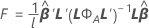
onde
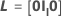
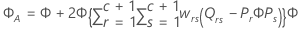
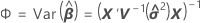
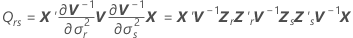
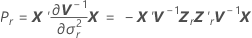
Notação
| Termo | Descrição |
|---|---|
| l | os graus de liberdade do numerador, que é o número de parâmetros no termo a ser testado |
| 0 | a matriz com 0 componentes |
| Il | a matriz identidade com dimensão l |
| c + 1 | o número de componentes de variância |
| wrs | (r, s)o componente da matriz de variância-covariância assintótica de  |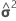
| V−1 | inverso da matriz de variância-covariância |
Para obter mais detalhes sobre a notação, vá para a seção Métodos.
Graus de liberdade do denominador
onde
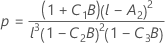
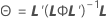
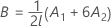
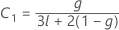
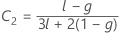
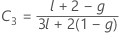
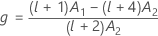
λ de Kenward e Roger
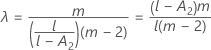
Se uma dessas condições não for verdadeira, então λ = 1.
Sob a hipótese nula, lambda × F é assintoticamente F distribuído com graus de liberdade DF Num, e DF Den. O cálculo do valor-p usa essa propriedade.
Aproximação de Satterthwaite
A aproximação de Satterthwaite é um método para testar a significância estatística em termos de efeito fixo.
Estatística F
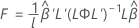
onde L e 
têm as mesmas definições que na aproximação de Kenward-Roger.
Graus de liberdade do denominador
O processo para a determinação dos graus de liberdade tem múltiplos passos.
-
Realize a decomposição espectral sobre a variância da estimativa do vetor de parâmetros do efeito fixo:
onde P é uma matriz ortogonal de autovetores e D é uma matriz diagonal de autovalores, para ambas as dimensões l × l.
-
Defina lr como a ra linha de P'L, r = 1, ..., l e seja
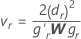onde dr é o ro elemento diagonal de D, W é a matriz de variância covariância assintótica
e gr é o vetor gradiente dos seguintes elementos:
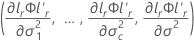
em que
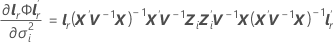
i = 1, …, c, e
-
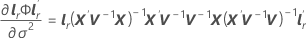
Permita que
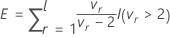
onde
é uma função indicadora que elimina termos com 
-
Os graus de liberdade do denominador dependem do valor de E.
- Se E > l, então, os graus de liberdade seguem:
- Senão, DF Den = 1
- Se E > l, então, os graus de liberdade seguem:
Graus de liberdade do numerador (DF Num)
| Efeito | DF |
|---|---|
| Fator fixo |  |
| Covariável | 1 |
| Interações que envolvem fatores fixos |  |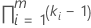
Notação
| Termo | Descrição |
|---|---|
| k | o número de níveis no termo de fator fixo |
| m | o número de fatores na interação |
Valor-p – Testes de efeitos fixos
Notação
| Termo | Descrição |
|---|---|
 | a função distribuição acumulada da distribuição-F com graus de liberdade igual a DF Num e DF Den, respectivamente |
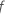 | o valor-F calculado para um termo |
