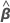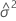Neste tópico
O modelo de efeitos mistos e o log-verossimilhança
A forma geral do modelo de efeitos mistos
Os modelos de efeito misto contêm efeitos fixos e aleatórios. A forma geral do modelo de efeitos mistos é:
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
Notação
| Termo | Descrição |
|---|---|
| y | o vetor n x 1 dos valores de resposta |
| X | a matriz de experimento n x p para os termos de efeito fixo, p ≤ n |
| β | um vetor p x 1 de parâmetros desconhecidos |
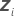 | a matriz de experimento n x mi para o  termo aleatório no modelo termo aleatório no modelo |
| μi | um vetor mi x 1 de variáveis de independentes de N(0,  ) ) |
| ε | um vetor n x 1 de variáveis independentes de N(0,  ) ) |
| n | o número de observações |
| p | o número de parâmetros em  |
| c | o número de termos aleatórios no modelo |
Matriz de variância-covariância
Com base no pressuposto do modelo para a forma geral do modelo de efeitos mistos, o vetor de resposta, y, tem uma distribuição normal multivariada com vetor médio Xβ e a seguinte matriz de variância-covariância:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
onde
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c são chamados componentes de variância.
Por fatoração da variância, você pode encontrar uma representação de H(θ), que está no cálculo da log-verossimilhança dos modelos de efeitos mistos.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
Notação
| Termo | Descrição |
|---|---|
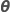 | 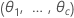 |
| θi | 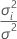 , a razão da variância do , a razão da variância do  termo aleatório sobre a variância do erro termo aleatório sobre a variância do erro |
Log-verossimilhança


Notação
| Termo | Descrição |
|---|---|
| H | In + θ1Z1Z'1 + ... + θcZcZ'c |
| |H| | o determinante de H |
| H-1 | o inverso de H |
| mi | o número de níveis para o  termo aleatório termo aleatório |
 | o erro do componente de variância |
| In | a matriz de identidade com n linhas e colunas |
Estimativa de máxima verossimilhança restrita (REML)
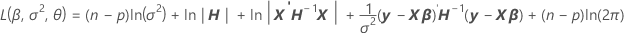
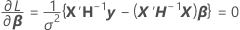
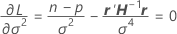
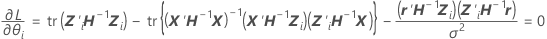
onde 
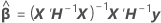
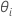 não pode ser resolvida explicitamente para a
não pode ser resolvida explicitamente para a 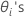 . O Minitab usa o método de Newton para estimar
. O Minitab usa o método de Newton para estimar 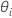 com as etapas a seguir:
com as etapas a seguir:
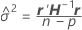
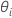 são as estimativas de razão de variância. O componente de variância para o
são as estimativas de razão de variância. O componente de variância para o  termo aleatório é como segue:
termo aleatório é como segue:

Notação
| Termo | Descrição |
|---|---|
| tr(·) | o traço da matriz |
| X' | a transposição do X |