Neste tópico
Ajustes condicionais
Os ajustes condicionais são as estimativas para os valores médios de resposta, tanto nas configurações de fator fixas como aleatórias dadas no conjunto de dados. Os ajustes condicionais são calculados a partir das equações ajustadas condicionais.
Ajuste SE
O erro padrão do ajuste (EP fit) estima a variação na resposta da média estimada para as configurações de variável especificadas. O cálculo do intervalo de confiança para a resposta média usa o erro padrão do ajuste. Os erros padrão são sempre não negativos.
DF para média condicional
Os graus de liberdade (DF) representam a quantidade de informações nos dados para estimar o intervalo de confiança da média de resposta.
Interpretação
Use o DF para comparar quanta informação está disponível sobre diferentes médias condicionais. Geralmente, mais graus de liberdade tornam o intervalo de confiança para a média mais estreito do que um intervalo com menos graus de liberdade. Como os erros padrão das médias para diferentes observações são diferentes, o intervalo de confiança para uma média com mais graus de liberdade não tem que ser mais estreito do que um intervalo de confiança para uma média com menos graus de liberdade.
Intervalo de confiança para a média condicional (IC de 95%)
Estes intervalos de confiança (IC) são amplitudes de valores que apresentam a probabilidade de conter as respostas médias condicionais correspondentes.
Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. Mas, se você extrair amostras várias vezes, uma determinada porcentagem dos intervalos de confiança resultantes conterá o parâmetro populacional desconhecido. A porcentagem destes intervalos de confiança que contém o parâmetro é o nível de confiança do intervalo.
O intervalo de confiança é composto pelas duas partes a seguir:
Interpretação
Use os intervalos de confiança para avaliar se as respostas médias condicionais são estatisticamente maiores do que, iguais a, ou menores do que um valor específico. Você também pode usar os intervalos de confiança para determinar uma amplitude de valores para as respostas médias condicionais desconhecidas correspondentes.
Resid condicional
Um resíduo (ei) é a diferença entre um valor observado (y) e o valor ajustado condicional correspondente, (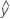 ).
).
Interpretação
Represente graficamente os resíduos para determinar se seu modelo é adequado e se atende as suposições de modelo de efeitos mistos. O exame dos resíduos pode fornecer informações úteis sobre quão bem o modelo se ajusta aos dados. Em geral, os resíduos devem ser distribuídos aleatoriamente, sem padrões óbvios e nenhum valor incomum. Se o Minitab determina que os dados incluem observações incomuns, ele identifica as observações na tabela Ajustes e Diagnósticos Condicionais para Observações Incomuns na saída. As observações que o Minitab rotula como incomuns não seguem bem a equação condicional proposta. No entanto, espera-se que você tenha algumas observações incomuns. Por exemplo, com base nos critérios de grandes resíduos, espera-se que aproximadamente 5% das observações sejam sinalizadas como tendo um resíduo grande.
Resíd. pdr.
O resíduo condicional padronizado é igual ao valor de um resíduo, (ei), dividido por uma estimativa de seu desvio padrão.
Interpretação
Use os resíduos condicionais padronizados para ajudar a detectar outliers. Resíduos condicionais padronizados maiores do que 2 e e menores do que -2 normalmente são considerados grandes. A tabela Ajustes e Diagnósticos Condicionais para Observações Incomuns identifica essas observações com um 'R'. As observações que o Minitab rotula não seguem bem a equação ajustada condicional proposta. No entanto, espera-se que você tenha algumas observações incomuns. Por exemplo, com base nos critérios de grandes resíduos condicionais padronizados, espera-se que aproximadamente 5% das observações sejam sinalizadas como tendo um grande resíduo padronizados.
Os resíduos condicionais padronizados são úteis porque resíduos condicionais brutos podem não ser bons indicadores de outliers. A variância de cada resíduo condicional bruto pode diferir pelos valores-x associados a ela. Esta variação desigual faz com que seja difícil avaliar as magnitudes dos resíduos condicionais brutos. A padronização dos resíduos condicionais soluciona esse problema convertendo as diferentes variâncias a uma escala comum.
