Um pesquisador testa a produção de seis variedades de alfafa em quatro campos selecionados aleatoriamente. A produção de cada variedade foi registrada para cada campo.
O pesquisador quer saber se a variedade de alfafa afeta o rendimento médio. O pesquisador tem 4 campos onde eles podem coletar dados. No entanto, o pesquisador quer ser capaz de modelar como as alfafas crescerão nos campos que não estão no experimento. Assim, o pesquisador faz com que o campo onde a alfafa cresce um fator aleatório. O pesquisador usa um modelo de efeitos mistos para avaliar os efeitos fixos e aleatórios juntos.
- Abra os dados das amostras Alfafa.MWX.
- Selecione .
- Em Respostas, insira Rendimento.
- Em Fatores aleatórios (obrigatórios), insira Campo.
- Em Fatores fixos, insira Variedade.
- Clique em Gráficos.
- Em Resíduos para gráficos, selecione Padronizado condicional.
- Em Gráficos de resíduos, selecione Quatro em um.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
Na tabela Componentes de Variância, o valor-p para Campo é 0,124. O teste de hipótese não mostra evidências de que o componente de variância é diferente de 0. O valor-p para o componente de variância de erro é de 0,003. Como o valor-p é menor do que o nível de significância de 0,05, o pesquisador pode concluir que o componente de variância para o erro não é 0.
O valor-p de aproximadamente 0 para o termo de fator fixo, Variedade, mostra que pelo menos um tipo de efeito sobre a produção de alfafa é significativamente diferente dos outros cinco tipos.
Os coeficientes para os efeitos principais representam a diferença entre cada nível médio e a média geral. Por exemplo, Variedade 1 está associada com um rendimento de alfafa que é de aproximadamente 0,385 unidades maior do que a média global. O valor-p de aproximadamente 0 para este coeficiente indica que o efeito da Variedade 1 sobre o rendimento é significativamente diferente de um outro efeito do nível do termo de Variedade. Para determinar quais os efeitos de nível são estatisticamente iguais, e quais efeitos de nível são estatisticamente diferentes, o pesquisador pretende fazer uma análise de comparação múltipla para o termo.
O valor R2 mostra que o modelo explica cerca de 92% da variação no rendimento. O valor de R-quadrado (adj) também é elevado, com um valor de aproximadamente 90,2%. O pesquisador usa esse valor para comparar os modelos que têm números diferentes de preditores.
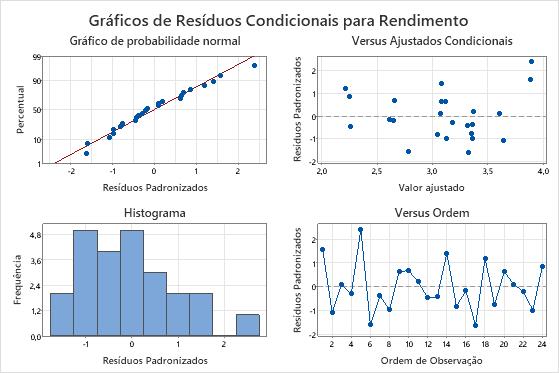
As observações 1 e 5 são observações incomuns porque elas têm resíduos padronizados superiores a 2. O pesquisador examina os dados para se certificar de que os valores de resposta para essas observações estão corretos.
Os resíduos no gráfico de probabilidade normal se aproximam de uma reta, e os pontos parecem estar dispersos aleatoriamente em torno de 0 no gráfico de resíduos versus ajustes.
Método
| Estimação de variância | Máxima verossimilhança restrita |
|---|---|
| GL para efeitos fixos | Kenward-Roger |
Informações dos Fatores
| Fator | Tipo | Níveis | Valores |
|---|---|---|---|
| Campo | Aleatório | 4 | 1; 2; 3; 4 |
| Variedade | Fixo | 6 | 1; 2; 3; 4; 5; 6 |
Componentes de Variância
| Fonte | Var | % do Total | EP de Var | Valor-Z | Valor-P |
|---|---|---|---|---|---|
| Campo | 0,077919 | 72,93% | 0,067580 | 1,152996 | 0,124 |
| Erro | 0,028924 | 27,07% | 0,010562 | 2,738613 | 0,003 |
| Total | 0,106843 |
Testes de Efeitos Fixos
| Termo | Num GL | Den GL | Valor F | Valor-P |
|---|---|---|---|---|
| Variedade | 5,00 | 15,00 | 26,29 | 0,000 |
Sumário do Modelo
| S | R2 | R2(aj) | AICc | BIC |
|---|---|---|---|---|
| 0,170071 | 92,33% | 90,20% | 12,54 | 13,52 |
Coeficientes
| Termo | Coef | EP de Coef | GL | Valor-T | Valor-P |
|---|---|---|---|---|---|
| Constante | 3,094583 | 0,143822 | 3,00 | 21,516692 | 0,000 |
| Variedade | |||||
| 1 | 0,385417 | 0,077626 | 15,00 | 4,965016 | 0,000 |
| 2 | 0,145417 | 0,077626 | 15,00 | 1,873287 | 0,081 |
| 3 | 0,107917 | 0,077626 | 15,00 | 1,390205 | 0,185 |
| 4 | -0,319583 | 0,077626 | 15,00 | -4,116938 | 0,001 |
| 5 | 0,395417 | 0,077626 | 15,00 | 5,093838 | 0,000 |
Valores Ajustados e Diagnósticos Marginais para Observações Atípicas
| Obs. | Rendimento | Ajuste | Resíd | Resíd Pad | |
|---|---|---|---|---|---|
| 1 | 4,100000 | 3,480000 | 0,620000 | 2,190221 | R |
| 5 | 4,220000 | 3,490000 | 0,730000 | 2,578808 | R |
Valores Ajustados e Diagnósticos Condicionais para Observações Atípicas
| Obs. | Rendimento | Ajuste | Resíd | Resíd Pad | |
|---|---|---|---|---|---|
| 5 | 4,220000 | 3,895339 | 0,324661 | 2,400733 | R |