Teste de Wilk
O teste estatístico, lambda de Wilk, é:
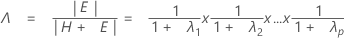
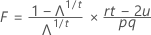
com pq e (rt – 2u) df.
Notação
| Termo | Descrição |
|---|---|
| H | matriz da hipótese |
| E | matriz do erro |
| p | número de respostas |
| q | df da hipótese |
| v | df para E |
| s | mín (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5, se p2 + q2 - 5 > 0 |
| t | 1 |
Seja λ1≥λ2≥λ3≥ . . . ≥λp os autovalores de (E** - 1) * H. As três primeiras estatísticas de teste podem ser expressas em termos de ambos os H e E ou estes autovalores.
A matriz H é uma matriz p x p que contém a soma de quadrados "entre" na diagonal para cada uma das variáveis de p. A matriz H é calculada como:

A matriz E é uma matriz p x p que contém a soma de quadrados "dentro" na diagonal para cada uma das variáveis de p. A matriz E é calculada como:
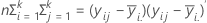
Nos três primeiros testes, a estatística F é exata, se s = 1 ou 2, caso contrário, é aproximada. O Minitab informa quando o teste é aproximado.
Teste Lawley-Hotelling
O teste estatístico, o traço Lawley-Hotelling, é:

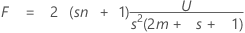
com s (2m + s + 1) e 2 (sn + 1) df.
Notação
| Termo | Descrição |
|---|---|
| H | matriz da hipótese |
| E | matriz do erro |
| p | número de respostas |
| q | df da hipótese |
| v | df para E |
| s | mín (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0,5 (p – q + 1) |
| u | 0,25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5, se p2 + q2 - 5 > 0 |
| t | 1 |
Seja λ1≥λ2≥λ3≥ . . . ≥λp os autovalores de (E** - 1) * H. As três primeiras estatísticas de teste podem ser expressas em termos de ambos os H e E ou estes autovalores.
A matriz H é uma matriz p x p que contém a soma de quadrados "entre" na diagonal para cada uma das variáveis de p. A matriz H é calculada como:

A matriz E é uma matriz p x p que contém a soma de quadrados "dentro" na diagonal para cada uma das variáveis de p. A matriz E é calculada como:
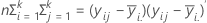
Nos três primeiros testes, a estatística F é exata, se s = 1 ou 2, caso contrário, é aproximada. O Minitab informa quando o teste é aproximado.
Teste de Pillai
O teste estatístico, traço de Pillai, é:
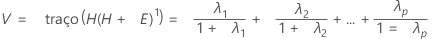

Notação
| Termo | Descrição |
|---|---|
| H | Matriz da hipótese |
| E | matriz do erro |
| p | número de respostas |
| q | df da hipótese |
| v | df para E |
| s | mín (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5, se p2 + q2 - 5 > 0 |
| t | 1 |
Seja λ1≥λ2≥λ3≥ . . . ≥λp os autovalores de (E** - 1) * H. As três primeiras estatísticas de teste podem ser expressas em termos de ambos os H e E ou estes autovalores.
A matriz H é uma matriz p x p que contém a soma de quadrados "entre" na diagonal para cada uma das variáveis de p. A matriz H é calculada como:

A matriz E é uma matriz p x p que contém a soma de quadrados "dentro" na diagonal para cada uma das variáveis de p. A matriz E é calculada como:
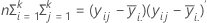
Nos três primeiros testes, a estatística F é exata, se s = 1 ou 2, caso contrário, é aproximada. O Minitab informa quando o teste é aproximado.
Teste da raiz máxima de Roy
Maior autovalor, λ1. Para concluir o teste, você deve usar gráficos especiais, chamados de gráficos de Heck, juntamente com os parâmetros s, m e n, para encontrar o nível de significância.
Consulte Heck1 para estes gráficos.
Notação
| Termo | Descrição |
|---|---|
| s | mín (p, q) |
| m | .5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
Seja λ1≥λ2≥λ3≥ . . . ≥λp os autovalores de (E** - 1) * H. As três primeiras estatísticas de teste podem ser expressas em termos de ambos os H e E ou estes autovalores.
- D.L. Heck (1960), "Charts of Some Upper Percentage Points of the Distribution of the Largest Characteristic Root," The Annals of Statistics, 625–642.
