Neste tópico
- Etapa 1: Teste a igualdade das médias de todas as respostas
- Etapa 2: Determine quais médias de resposta têm as maiores diferenças para cada fator
- Etapa 3: Avalie as diferenças entre as médias do grupo
- Etapa 4: Avalie os resultados univariados para examinar as respostas individuais
- Etapa 5: Determinar se o modelo atende às suposições da análise
Etapa 1: Teste a igualdade das médias de todas as respostas
- Valor-p ≤ α: as diferenças entre algumas das médias são estatisticamente significativas
- Se o valor-p for menor ou igual ao nível de significância, é possível concluir que as diferenças entre as médias são estatisticamente significativas.
- Valor-p > α: as diferenças entre algumas das médias não são estatisticamente significativas
- Se o valor-p for maior que o nível de significância, não é possível concluir que as diferenças entre as médias são estatisticamente significativas. Talvez seja necessário reajustar o modelo sem o termo.
- Se um efeito principal for significativo, as médias de nível para o fator são significativamente diferentes umas das outras em todas as respostas em seu modelo.
- Se um termo de interação for significativo, os efeitos de cada fator são diferentes em cada nível de outros fatores em todas as respostas em seu modelo. Por esta razão, você não deve analisar os efeitos individuais de termos envolvidos nas interações significativas de ordem superior.
Testes de MANOVA para Método
| Estatística de teste | GL | ||||
|---|---|---|---|---|---|
| Critério | F | Núm. | Denom. | P | |
| De Wilks | 0,63099 | 16,082 | 2 | 55 | 0,000 |
| Lawley-Hotelling | 0,58482 | 16,082 | 2 | 55 | 0,000 |
| De Pillai | 0,36901 | 16,082 | 2 | 55 | 0,000 |
| De Roy | 0,58482 | ||||
Testes de MANOVA para Fábrica
| Estatística de teste | GL | ||||
|---|---|---|---|---|---|
| Critério | F | Núm. | Denom. | P | |
| De Wilks | 0,89178 | 1,621 | 4 | 110 | 0,174 |
| Lawley-Hotelling | 0,11972 | 1,616 | 4 | 108 | 0,175 |
| De Pillai | 0,10967 | 1,625 | 4 | 112 | 0,173 |
| De Roy | 0,10400 | ||||
Testes de MANOVA para Método*Fábrica
| Estatística de teste | GL | ||||
|---|---|---|---|---|---|
| Critério | F | Núm. | Denom. | P | |
| De Wilks | 0,85826 | 2,184 | 4 | 110 | 0,075 |
| Lawley-Hotelling | 0,16439 | 2,219 | 4 | 108 | 0,072 |
| De Pillai | 0,14239 | 2,146 | 4 | 112 | 0,080 |
| De Roy | 0,15966 | ||||
Principais resultados: P
Os valores-p para o método de produção são estatisticamente significativos para o nível de significância de 0,10. Os valores-p para a fábrica não são significativos no nível de 0,10 de significância para qualquer um dos testes. Os valores-p para a interação entre fábrica e o método são estatisticamente significativos ao nível de significância de 0,10. Como a interação é estatisticamente significativa, o efeito do método depende da fábrica.
Etapa 2: Determine quais médias de resposta têm as maiores diferenças para cada fator
Utilize a auto análise para avaliar o modo como as médias de resposta variam entre os diferentes níveis dos termos modelo. Você deve se concentrar em autovetores que correspondem a autovalores elevados. Para exibir a auto análise, acesse e selecione Auto Análise (Autovalores e Autovetores) em Exibição dos Resultados.
Análise de Autovalores e Autovetores para Método
| Autovalor | 0,5848 | 0,00000 |
|---|---|---|
| Proporção | 1,0000 | 0,00000 |
| Acumulado | 1,0000 | 1,00000 |
| Autovetor | 1 | 2 |
|---|---|---|
| Classificação de Usabilidade | 0,144062 | -0,07870 |
| Classificação de Qualidade | -0,003968 | 0,13976 |
Resultados principais: autovalor, autovetor
Nestes resultados, o primeiro autovalor para o método (0,5848) é maior do que o segundo autovalor (0,00000). Portanto, você deve colocar maior importância no primeiro autovetor. O primeiro autovetor para o método é 0,144062, -0,003968. O maior valor absoluto dentro deste vetor é para a classificação de usabilidade. Isto sugere que os meios para a usabilidade apresentam a maior variação entre os níveis do fator de método. Esta informação é útil para avaliar a tabela de médias.
Etapa 3: Avalie as diferenças entre as médias do grupo
Use a tabela Médias para entender as diferenças estatisticamente significativas entre os níveis de fatores em seus dados. A média de cada grupo fornece uma estimativa de cada média da população. Procure por diferenças entre médias de grupo para termos que são estatisticamente significativos.
Para efeitos principais, a tabela apresenta os grupos dentro de cada fator e suas médias. Para efeitos de interação, a tabela apresenta todas as combinações possíveis dos grupos. Se um termo de interação for estatisticamente significativo, não interprete os efeitos principais sem considerar os efeitos da interação.
Para exibir as médias, acesse , selecione Análise de variância univariada, e insira os termos em Exibir médias de mínimos quadrados correspondentes aos termos.
Médias dos Mínimos quadrados para respostas
| Classificação de Usabilidade | Classificação de Qualidade | |||
|---|---|---|---|---|
| Média | EP Média | Média | EP Média | |
| Método | ||||
| Método 1 | 4,819 | 0,165 | 5,242 | 0,193 |
| Método 2 | 6,212 | 0,179 | 6,026 | 0,211 |
| Fábrica | ||||
| Fábrica A | 5,708 | 0,192 | 5,833 | 0,226 |
| Fábrica B | 5,493 | 0,232 | 5,914 | 0,273 |
| Fábrica C | 5,345 | 0,206 | 5,155 | 0,242 |
| Método*Fábrica | ||||
| Método 1 Fábrica A | 4,667 | 0,272 | 5,417 | 0,319 |
| Método 1 Fábrica B | 4,700 | 0,298 | 5,400 | 0,350 |
| Método 1 Fábrica C | 5,091 | 0,284 | 4,909 | 0,334 |
| Método 2 Fábrica A | 6,750 | 0,272 | 6,250 | 0,319 |
| Método 2 Fábrica B | 6,286 | 0,356 | 6,429 | 0,418 |
| Método 2 Fábrica C | 5,600 | 0,298 | 5,400 | 0,350 |
Resultados principais: Média
Nestes resultados, a tabela Médias mostra como a usabilidade média e as classificações de qualidade variam de acordo com o método, instalação e a interação método*instalação. O método e o termo de interação são estatisticamente significativos ao nível 0,10. A tabela mostra que o método 1 e o método 2 estão associados a classificações de usabilidade médias de 4,819 e 6,212, respectivamente. A diferença entre estas médias é maior do que a diferença entre as médias correspondentes para classificação da qualidade. Isto confirma a interpretação da auto análise (autovalores e autovetores).
No entanto, como o termo de interação Método*Instalação é estatisticamente significativo, não interprete os efeitos principais sem considerar os efeitos da interação. Por exemplo, a tabela para o termo de interação mostra que, com o método 1, a instalação C está associada com a mais alta classificação de usabilidade e a mais baixa classificação qualidade. No entanto, com o método 2, a instalação A está associada com a classificação de usabilidade mais alta e uma classificação de qualidade que é quase igual à classificação de qualidade mais alta.
Etapa 4: Avalie os resultados univariados para examinar as respostas individuais
Quando você realizar MANOVA generalizada, você pode optar por calcular as estatísticas univariadas para examinar as respostas individuais. Os resultados univariados podem fornecer uma compreensão mais intuitiva das relações em seus dados. No entanto, os resultados univariados podem diferir dos resultados multivariados.
Para exibir os resultados univariados, acesse e selecione Análise de variância univariada em Exibição dos Resultados.
- Valor-p ≤ α: a associação é estatisticamente significativa
- Se o valor-p for menor ou igual ao nível de significância, é possível concluir que há uma associação estatisticamente significativa entre a variável de resposta e o termo.
- Valor-p > α: a associação não é estatisticamente significativa
- Se o valor-p for maior ou igual ao nível de significância, não é possível concluir que há uma associação estatisticamente significativa entre a variável de resposta e o termo. Talvez seja necessário reajustar o modelo sem o termo.
- Se um fator categórico é significativo, é possível concluir que nem todas as médias de nível são iguais.
- Se um termo de interação é significativo, a relação entre um fator e a resposta depende dos outros fatores do termo. Neste caso, você não deve interpretar os principais efeitos sem considerar o efeito da interação.
- Se uma covariável for estatisticamente significativa, é possível concluir que as mudanças no valor da covariável estejam associadas a mudanças no valor médio da resposta.
- Se um termo polinomial for significativo, é possível concluir que os dados contêm curvatura.
Análise de Variância para Classificação de Usabilidade, usando SQ Ajustado para Testes
| Fonte | GL | SQ Seq | SQ (Aj.) | QM (Aj.) | F | P |
|---|---|---|---|---|---|---|
| Método | 1 | 31,264 | 29,074 | 29,0738 | 32,72 | 0,000 |
| Fábrica | 2 | 1,366 | 1,499 | 0,7495 | 0,84 | 0,436 |
| Método*Fábrica | 2 | 7,099 | 7,099 | 3,5494 | 3,99 | 0,024 |
| Erro | 56 | 49,754 | 49,754 | 0,8885 | ||
| Total | 61 | 89,484 |
Análise de Variância para Classificação de Qualidade, usando SQ Ajustado para Testes
| Fonte | GL | SQ Seq | SQ (Aj.) | QM (Aj.) | F | P |
|---|---|---|---|---|---|---|
| Método | 1 | 8,8587 | 9,2196 | 9,2196 | 7,53 | 0,008 |
| Fábrica | 2 | 6,7632 | 7,0572 | 3,5286 | 2,88 | 0,064 |
| Método*Fábrica | 2 | 0,7074 | 0,7074 | 0,3537 | 0,29 | 0,750 |
| Erro | 56 | 68,5900 | 68,5900 | 1,2248 | ||
| Total | 61 | 84,9194 |
Principais resultados: P
Nestes resultados, o valor de p para o efeito principal do método e o efeito da interação método*planta são estatisticamente significativos ao nível de 0,10 no modelo de classificação para a usabilidade. Os efeitos principais de ambos método e planta são estatisticamente significativos no modelo de classificação de qualidade. Você pode concluir que as mudanças nessas variáveis estão associadas às alterações nas variáveis de resposta.
Etapa 5: Determinar se o modelo atende às suposições da análise
Use os gráficos de resíduos para ajudar a determinar se o modelo é adequado e satisfaz aos pressupostos da análise. Se os pressupostos não forem satisfeitos, o modelo pode não ajustar bem os dados e você deve ter cautela ao interpretar os resultados.
Quando você executa MANOVA generalizada, o Minitab exibe gráficos de resíduos para todas as variáveis de resposta que estão em seu modelo. Você deve determinar se os gráficos de resíduos para todas as variáveis de resposta indicam que o modelo satisfazem aos pressupostos.
Para obter mais informações sobre como lidar com os padrões nos gráficos residuais, vá para Gráficos de resíduos para MANOVA generalizada e clique no nome do gráfico residual na lista na parte superior da página.
Gráficos de resíduos versus de ajustes
Use o gráfico de resíduos versus ajustes para verificar a pressuposição de que os resíduos são aleatoriamente distribuídos e têm variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Curvilíneo | Um termo de ordem mais alta ausente |
| Um ponto que está distante de zero | Um outlier |
| Um ponto que é distante dos outros pontos na direção x | Um ponto influente |
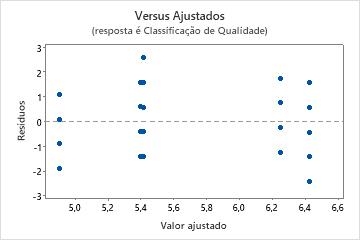
Gráfico de resíduos versus ordem
Tendência
Deslocamento
Ciclo
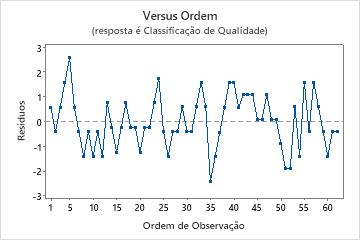
Gráficos de probabilidade normal dos resíduos
Use o gráfico de probabilidade normal de resíduos para verificar a pressuposição de que os resíduos são distribuídos normalmente. O gráfico de probabilidade normal dos resíduos deve seguir aproximadamente uma linha reta.
| Padrão | O que o padrão pode indicar |
|---|---|
| Não é uma linha reta | Não normalidade |
| Um ponto que está distante da linha | Um outlier |
| Alteração de inclinação | Uma variável não identificada |