Médias
A tabela de médias apresenta as médias ajustadas das observações dentro de grupos com base em uma ou mais variáveis categóricas. As médias ajustadas usam os mínimos quadrados para predizer os valores médios de resposta de um experimento balanceado.
Interpretação
As médias ajustadas estimam a resposta média em diferentes níveis de um fator, enquanto a calcula a média sobre os níveis dos outros fatores.
Use a tabela Médias para entender as diferenças estatisticamente significativas entre os níveis de fatores em seus dados. A média de cada grupo fornece uma estimativa de cada média da população. Procure por diferenças entre médias de grupo para termos que são estatisticamente significativos.
Para efeitos principais, a tabela apresenta os grupos dentro de cada fator e suas médias. Para efeitos de interação, a tabela apresenta todas as combinações possíveis dos grupos. Se um termo de interação for estatisticamente significativo, não interprete os efeitos principais sem considerar os efeitos da interação.
Nestes resultados, a tabela Médias mostra como a usabilidade média e as classificações de qualidade variam de acordo com o método, instalação e a interação método*instalação. O método e o termo de interação são estatisticamente significativos ao nível 0,10. A tabela mostra que o método 1 e o método 2 estão associados a classificações de usabilidade médias de 4,819 e 6,212, respectivamente. A diferença entre estas médias é maior do que a diferença entre as médias correspondentes para classificação da qualidade. Isto confirma a interpretação da auto análise (autovalores e autovetores).
No entanto, como o termo de interação Método*Instalação é estatisticamente significativo, não interprete os efeitos principais sem considerar os efeitos da interação. Por exemplo, a tabela para o termo de interação mostra que, com o método 1, a instalação C está associada com a mais alta classificação de usabilidade e a mais baixa classificação qualidade. No entanto, com o método 2, a instalação A está associada com a classificação de usabilidade mais alta e uma classificação de qualidade que é quase igual à classificação de qualidade mais alta.
Médias dos Mínimos quadrados para respostas
| Classificação de Usabilidade | Classificação de Qualidade | |||
|---|---|---|---|---|
| Média | EP Média | Média | EP Média | |
| Método | ||||
| Método 1 | 4,819 | 0,165 | 5,242 | 0,193 |
| Método 2 | 6,212 | 0,179 | 6,026 | 0,211 |
| Fábrica | ||||
| Fábrica A | 5,708 | 0,192 | 5,833 | 0,226 |
| Fábrica B | 5,493 | 0,232 | 5,914 | 0,273 |
| Fábrica C | 5,345 | 0,206 | 5,155 | 0,242 |
| Método*Fábrica | ||||
| Método 1 Fábrica A | 4,667 | 0,272 | 5,417 | 0,319 |
| Método 1 Fábrica B | 4,700 | 0,298 | 5,400 | 0,350 |
| Método 1 Fábrica C | 5,091 | 0,284 | 4,909 | 0,334 |
| Método 2 Fábrica A | 6,750 | 0,272 | 6,250 | 0,319 |
| Método 2 Fábrica B | 6,286 | 0,356 | 6,429 | 0,418 |
| Método 2 Fábrica C | 5,600 | 0,298 | 5,400 | 0,350 |
EP Média
O erro padrão da média (SE Média) estima a variabilidade entre as médias ajustadas que você obteria se você tivesse extraído repetidas amostras da mesma população por repetidas vezes.
Por exemplo, você tem um tempo médio de entrega de 3,80 dias, com um desvio padrão de 1,43 dias, a partir de uma amostra aleatória de 312 tempos de entrega. Estes números produzem um erro padrão da média de 0,08 dias (1,43 dividido pela raiz quadrada de 312). Se você extraiu várias amostras aleatórias do mesmo tamanho e da mesma população, o desvio padrão dessas diferentes médias de amostra seria de cerca de 0,08 dias.
Interpretação
Use o erro padrão da média para determinar o quão precisamente a média ajustada estima a média da população.
Um valor menor do erro padrão da média indica uma estimativa mais precisa da média da população. Normalmente, um desvio padrão maior resulta em um erro padrão maior da média e em uma estimativa menos precisa da média da população. Um tamanho amostral maior resulta em um erro padrão menor da média e uma estimativa mais precisa da média da população.
Média (covariável)
A média da covariável é a média dos dados, que é a soma de todas as observações divididas pelo número de observações. A média sumariza os valores das amostras com um único valor que representa o centro dos dados.
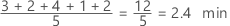
Interpretação
Use a média para descrever a covariável com um único valor que representa o centro dos dados.
Desvio padrão (StDev)
O desvio padrão é a medida mais comum de dispersão, ou quão dispersos os dados estão da média. O símbolo σ (sigma) é muitas vezes usado para representar o desvio padrão da população. O símbolo s é usado para representar o desvio padrão de uma amostra.
Interpretação
- Aproximadamente 68% dos valores caem dentro de um desvio padrão da média.
- 95% dos valores caem dentro de dois desvios padrão.
- 99,7% dos valores caem dentro de três desvios padrão.
O desvio padrão de um grupo é uma estimativa do desvio padrão da população daquele grupo. Os desvios padrão são usados para calcular os intervalos de confiança e os valores dep. Desvios padrão da amostra maiores resultam em intervalos de confiança (mais largos) menos precisos e poder estatístico menor.
A análise de variância pressupõe que os desvios padrão da população para todos os níveis são iguais. Se não for possível assumir variâncias iguais, use a ANOVA de Welch, que é uma opção para ANOVA com 1 fator que está disponível no Minitab Statistical Software.
