Neste tópico
Modelo de ANOVA completamente aninhada
O modelo da ANOVA aninhada para um experimento balanceado com dois fatores aleatórios (A e B) é:
yijk = μ .. + α i+ β j(i) +εijk
em que α i, β j(i) e ε ijksão variáveis normais aleatórias independentes com as expectativas 0 e variâncias σ2α , σ2β , e σ2, respectivamente.
Os parâmetros são estimados pelo seguinte
μ .. = y̅...
α i = yi..− y̅...
β j(i) = yij.− y̅i..
em que y̅... = média de todas as observações , yi..= média de observações no iésimo nível do fator A, yij. = é a média das observações para o ésimo nível do fator B no iésimo nível do fator A. O parâmetro β j(i) é o efeito específico de B quando A está no nível i.
- J. Neter, W. Wasserman and M.H. Kutner (1985). Modelos estatísticos lineares aplicados. Segunda edição. Irwin, Inc.
Soma dos quadrados sequencial
A soma das distâncias ao quadrado. SS total é a variação total nos dados. SS (A) e SS (B) representam a quantidade de variação da média de nível de fator estimado em torno da média global. Eles também são conhecidos como a soma dos quadrados para o fator A ou fator B. SS Erro é a quantidade de variação das observações de seus valores ajustados. Os cálculos são:
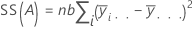
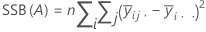
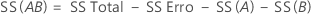


O Minitab fornece a somas dos quadrados sequencial, que depende da ordem em que os fatores são inseridos no modelo. Ela é a parte única da Regressão SS explicada por um fator, considerando-se todos os fatores inseridos anteriormente.
Notação
| Termo | Descrição |
|---|---|
| a | número de níveis no fator A |
| b | número de níveis no fator B |
| n | número total de ensaios |
| yi.. | média do io nível de fator do fator A |
| y | média global de todas as observações |
| y.j. | média do jo nível de fator do fator B |
| yij | média de observações no io nível do fator A e o jo nível do fator B |
Graus de liberdade (DF)
Para um modelo de ANOVA completamente aninhada com dois fatores, A e B, os graus de liberdade são:




onde a = número de níveis no fator A, b = o número de níveis no fator B, e N é o número de ensaios.
Quadrado Médio (MS)
Fórmulas

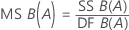

F
Estas são as fórmulas para a estatística F de um modelo com fatores aleatórios.
Fórmulas
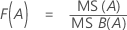
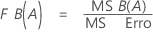
Valor-p – Tabela Análise de Variância
O valor-p é a probabilidade que é calculada a partir de uma distribuição-f com graus de liberdade (DF) como a seguir:
- DF do numerador
- soma dos graus de liberdade para o termo ou os termos do teste
- DF do denominador
- graus de liberdade para erro
Fórmula
1 − P(F ≤ fj)
Notação
| Termo | Descrição |
|---|---|
| P(F ≤ f) | função de distribuição acumulada para a distribuição F |
| f | estatística F de teste |
Componentes da variância
Calculado para fatores aleatórios. O modelo aninhado com dois fatores aleatórios é:
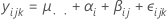
onde, αi, βj(i) e εijk são variáveis aleatórias normais independentes. As variáveis são normalmente distribuídas com média zero e variâncias dadas por V(αi) = σ2α,V(βj) = σ2β e V(εijk) = σ2. É pressuposto que todo o bj(i) tem a mesma variância que σ2β, σ2α, σ2β, σ2αβ, σ2 são chamados componentes de variância.
Quadrados médios esperados
Para um modelo com dois fatores aleatórios, A e B, os quadrados médios esperados são:
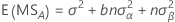


Estatística-f para modelos com fatores aleatórios
Como as estatísticas F são calculadas na saída da ANOVA
Cada estatística F é uma razão de quadrados médios. O numerador é o quadrado médio para o termo. O denominador é escolhido de tal modo que o valor esperado do quadrado médio do numerador difere do valor esperado do quadrado médio do denominador apenas pelo efeito de interesse. O efeito para um termo aleatório é representado pelo componente de variância do termo. O efeito para um termo fixo é representado pela soma dos quadrados dos componentes do modelo associada a esse termo dividida por seus graus de liberdade. Por conseguinte, uma estatística F elevada indica um efeito significativo.
Quando todos os termos do modelo são fixos, o denominador para cada estatística F é o quadrado médio do erro (MSE). No entanto, para modelos que incluem termos aleatórios, o MSE não é sempre o quadrado médio correto. Os quadrados médios esperados (EMS) podem ser utilizados para determinar qual é apropriado para o denominador.
Exemplo
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Tela | (4) + 2.0000(3) + Q[1] |
| (2) Tec | (4) + 2,0000(3) + 4,0000(2) |
| (3) tela * Tec | (4) + 2,0000(3) |
| (4) Erro | (4) |
Um número entre parênteses indica um efeito aleatório associado ao termo relacionado ao lado do número de fonte. (2) representa o efeito aleatório de Tech, (3) representa o efeito aleatório da interação de Screen*Tech, e (4) representa o efeito aleatório de Erro. O EMS para Erro é o efeito do termo de erro. Além disso, o EMS para Screen*Tech é o efeito do termo de erro mais duas vezes o efeito da interação Screen*Tech.
Para calcular a estatística F para Screen*Tech, o quadrado médio para Screen*Tech é dividido pelo quadrado médio do erro, de forma que o valor esperado do numerador (EMS para Screen*Tech = (4) + 2,0000 (3) ) difere do valor esperado do denominador (EMS para o erro = (4)) apenas pelo efeito da interação (2,0000 (3)). Por isso, uma estatística F elevada indica uma interação Screen*Tech significativa.
Um número com Q[ ] indica um efeito fixo associado ao termo relacionado ao lado do número de fonte. Por exemplo, Q[1] é o efeito fixo de Tela. O EMS para Tela é o efeito do termo de erro mais duas vezes o efeito da interação Tela*Tec mais uma constante vezes o efeito da tela. Q[1] é igual a (b*n * (soma ((coeficientes para níveis de Tela)**2)) dividida por (a - 1), em que a e b são o número de níveis de Tela e Tech, respectivamente, e n é o número de replicações.
Para calcular a primeira estatística para Tela * Tec, a média quadrada para Tela * Tec é dividida pela média quadrada do erro de forma que o valor esperado do numerador (EMS para Tela * Tec = (4) + 2,0000(3) + Q[1]) difere do valor esperado do denominador (EMS para Tela * Tec = (4) + 2,0000(3)) somente pelo efeito de Tela Q[1]). Por isso, uma estatística F elevada indica uma interação Screen significativa.
Por que a saída da ANOVA inclui um "x" ao lado de um valor p na tabela ANOVA e o rótulo "Não é um teste F exato"?
Um teste F exato para um termo é um dos quais o valor esperado da média quadrada do numerador difere do valor esperado da média quadrada do denominador apenas pelo componente de variância ou o fator de interesse fixo.
Algumas vezes, porém, não é possível calcular a média quadrada. Nesse caso, o Minitab usa uma média quadrada que resulte em um teste F aproximado e exibe "x" ao lado do valor de p para identificar que o teste F não é exato.
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Suplemento | (4) + 1,7500(3) + Q[1] |
| (2) Lago | (4) + 1,7143(3) + 5,1429(2) |
| (3) Suplemento * Lago | (4) + 1,7500(3) |
| (4) Erro | (4) |
A estatística F para o suplemento é a média quadrada de Suplement dividida pela média quadrada da interação Supplement*Lake. Se o efeito para Suplement for pequeno demais, o valor esperado do numerador é igual ao valor esperado do denominador. Este é um exemplo de um teste F exato.
Observe, no entanto, que, para um efeito pequeno demais de Lake, não existem médias quadradas de forma que o valor esperado do numerador é igual ao valor esperado do denominador. Portanto, o Minitab usa um teste F aproximado. Neste exemplo, a média quadrada de Lake é dividida pela média quadrado para a interação Supplement*Lake. Isto resulta em um valor esperado do numerador aproximadamente igual ao do denominador caso o efeito de Lake seja muito pequeno.
Sobre a mensagem "Denominador do teste F zero ou não definido"
- Não existe pelo menos um grau de liberdade para erro.
-
Os valores de MS ajustados são muito pequenos e, portanto, não há de precisão suficiente para exibir o F e os valoresdep. Como solução, multiplique a coluna de resposta por 10. Em seguida, realize o mesmo modelo de regressão, mas, em vez disso, use esta nova coluna de resposta para a resposta.
Observação
Multiplicar os valores de resposta por 10 não afetará os valores de F e de p que o Minitab exibe na saída. No entanto, a posição decimal será afetada na saída restante, especificamente, as colulas das somas dos quadrados sequenciais, Adj SS, Adj MS, Ajuste, erro padrão dos ajustes e dos resíduos.
Como as estatísticas F são calculadas na saída da ANOVA
Cada estatística F é uma razão de quadrados médios. O numerador é o quadrado médio para o termo. O denominador é escolhido de tal modo que o valor esperado do quadrado médio do numerador difere do valor esperado do quadrado médio do denominador apenas pelo efeito de interesse. O efeito para um termo aleatório é representado pelo componente de variância do termo. O efeito para um termo fixo é representado pela soma dos quadrados dos componentes do modelo associada a esse termo dividida por seus graus de liberdade. Por conseguinte, uma estatística F elevada indica um efeito significativo.
Quando todos os termos do modelo são fixos, o denominador para cada estatística F é o quadrado médio do erro (MSE). No entanto, para modelos que incluem termos aleatórios, o MSE não é sempre o quadrado médio correto. Os quadrados médios esperados (EMS) podem ser utilizados para determinar qual é apropriado para o denominador.
Exemplo
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Tela | (4) + 2.0000(3) + Q[1] |
| (2) Tec | (4) + 2,0000(3) + 4,0000(2) |
| (3) tela * Tec | (4) + 2,0000(3) |
| (4) Erro | (4) |
Um número entre parênteses indica um efeito aleatório associado ao termo relacionado ao lado do número de fonte. (2) representa o efeito aleatório de Tech, (3) representa o efeito aleatório da interação de Screen*Tech, e (4) representa o efeito aleatório de Erro. O EMS para Erro é o efeito do termo de erro. Além disso, o EMS para Screen*Tech é o efeito do termo de erro mais duas vezes o efeito da interação Screen*Tech.
Para calcular a estatística F para Screen*Tech, o quadrado médio para Screen*Tech é dividido pelo quadrado médio do erro, de forma que o valor esperado do numerador (EMS para Screen*Tech = (4) + 2,0000 (3) ) difere do valor esperado do denominador (EMS para o erro = (4)) apenas pelo efeito da interação (2,0000 (3)). Por isso, uma estatística F elevada indica uma interação Screen*Tech significativa.
Um número com Q[ ] indica um efeito fixo associado ao termo relacionado ao lado do número de fonte. Por exemplo, Q[1] é o efeito fixo de Tela. O EMS para Tela é o efeito do termo de erro mais duas vezes o efeito da interação Tela*Tec mais uma constante vezes o efeito da tela. Q[1] é igual a (b*n * (soma ((coeficientes para níveis de Tela)**2)) dividida por (a - 1), em que a e b são o número de níveis de Tela e Tech, respectivamente, e n é o número de replicações.
Para calcular a primeira estatística para Tela * Tec, a média quadrada para Tela * Tec é dividida pela média quadrada do erro de forma que o valor esperado do numerador (EMS para Tela * Tec = (4) + 2,0000(3) + Q[1]) difere do valor esperado do denominador (EMS para Tela * Tec = (4) + 2,0000(3)) somente pelo efeito de Tela Q[1]). Por isso, uma estatística F elevada indica uma interação Screen significativa.
Por que a saída da ANOVA inclui um "x" ao lado de um valor p na tabela ANOVA e o rótulo "Não é um teste F exato"?
Um teste F exato para um termo é um dos quais o valor esperado da média quadrada do numerador difere do valor esperado da média quadrada do denominador apenas pelo componente de variância ou o fator de interesse fixo.
Algumas vezes, porém, não é possível calcular a média quadrada. Nesse caso, o Minitab usa uma média quadrada que resulte em um teste F aproximado e exibe "x" ao lado do valor de p para identificar que o teste F não é exato.
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Suplemento | (4) + 1,7500(3) + Q[1] |
| (2) Lago | (4) + 1,7143(3) + 5,1429(2) |
| (3) Suplemento * Lago | (4) + 1,7500(3) |
| (4) Erro | (4) |
A estatística F para o suplemento é a média quadrada de Suplement dividida pela média quadrada da interação Supplement*Lake. Se o efeito para Suplement for pequeno demais, o valor esperado do numerador é igual ao valor esperado do denominador. Este é um exemplo de um teste F exato.
Observe, no entanto, que, para um efeito pequeno demais de Lake, não existem médias quadradas de forma que o valor esperado do numerador é igual ao valor esperado do denominador. Portanto, o Minitab usa um teste F aproximado. Neste exemplo, a média quadrada de Lake é dividida pela média quadrado para a interação Supplement*Lake. Isto resulta em um valor esperado do numerador aproximadamente igual ao do denominador caso o efeito de Lake seja muito pequeno.
Sobre a mensagem "Denominador do teste F zero ou não definido"
- Não existe pelo menos um grau de liberdade para erro.
-
Os valores de MS ajustados são muito pequenos e, portanto, não há de precisão suficiente para exibir o F e os valoresdep. Como solução, multiplique a coluna de resposta por 10. Em seguida, realize o mesmo modelo de regressão, mas, em vez disso, use esta nova coluna de resposta para a resposta.
Observação
Multiplicar os valores de resposta por 10 não afetará os valores de F e de p que o Minitab exibe na saída. No entanto, a posição decimal será afetada na saída restante, especificamente, as colulas das somas dos quadrados sequenciais, Adj SS, Adj MS, Ajuste, erro padrão dos ajustes e dos resíduos.
