Neste tópico
Modelo MLG
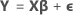
Notação
| Termo | Descrição |
|---|---|
| Y | vetor de respostas |
| X | matriz do experimento |
| β | vetor de parâmetros |
| ε | vetor de variáveis aleatórias normais independentes |
Matriz do experimento
O Modelo Linear Generalizado usa uma abordagem de regressão para ajustar o modelo que você especificar. Primeiro, o Minitab cria uma matriz de experimento a partir dos fatores e covariáveis e do modelo que você especificar. As colunas desta matriz são os preditores para a regressão.
A matriz do experimento tem n linhas, onde n = número de observações e vários blocos de colunas, o que corresponde aos termos do modelo. O primeiro bloco é para a constante e contém apenas uma coluna, uma coluna para todos eles. O bloco para uma covariável também contém apenas uma coluna, a própria coluna covariável. O bloco de colunas para um fator contém colunas, em que r = graus de liberdade para o fator, e eles são codificados como mostrado no exemplo abaixo.
Suponha que A seja um fator com 4 níveis. Ele possui 3 graus de liberdade e seu bloco contém 3 colunas, A1, A2 e A3.
| Nível de A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | –1 | –1 | –1 |
Suponha que o fator B tem 3 níveis aninhados dentro de cada nível de A. Então seu bloco contém (3 - 1) x 4 = 8 colunas, chame-as de B11, B12, B21, B22, B31, B32, B41, B42, codificadas como a seguir:
| Nível de A | Nível de B | B11 | B12 | B21 | B22 | B31 | B32 | B41 | B42 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 3 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 0 | –1 | –1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | –1 |
Para calcular as colunas para um termo de interação, basta multiplicar todas as colunas correspondentes para os fatores e/ou covariáveis na interação. Por exemplo, suponha que um fator tem 6 níveis, C tem 3 níveis, D tem 4 níveis e Z e W são covariáveis. Em seguida, o termo A * C * D * Z * W * W tem 5 x 2 x 3 x 1 x 1 x 1 = 30 colunas. Para obtê-las, multiplique cada coluna de A por cada de C, por cada de D, pelas covariáveis Z uma vez e W duas vezes.
Transformação Box-Cox
A transformação de Box-Cox seleciona valores de lambda, conforme mostrado a seguir, que minimizam a soma dos quadrados dos resíduos. A transformação resultante é Y λ quando λ ≠ 0 e ln(Y) quando λ = 0. Quando λ < 0, o Minitab também multiplica a resposta transformada por -1 para manter a ordem da resposta não transformada.
O Minitab pesquisa um valor ideal entre −2 e 2. Os valores que estão fora desse intervalo podem não resultar em um ajuste melhor.
A seguir estão algumas transformações comuns onde Y é a transformação dos dados Y:
| Valor lambda (λ) | Transformação |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 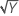 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Regressão ponderada
A regressão de mínimos quadrados ponderada é um método para lidar com as observações que têm variâncias não constantes. Se as variâncias são não constantes, observações com:
- grandes variâncias devem ser dadas em relação a pesos pequenos
- pequenas variâncias devem ser dadas em relação a pesos grandes
A escolha comum de pesos é o inverso da variância do erro puro na resposta.
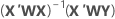
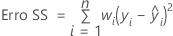
Notação
| Termo | Descrição |
|---|---|
| X | matriz do experimento |
| X' | transposição da matriz do experimento |
| W | uma matriz n x n com os pesos na diagonal |
| Y | vetor de valores de resposta |
| n | número de observações |
| wi | peso para a ia observação |
| yi | valor da resposta para a ia observação |
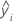 | valor ajustado para a ia observação |
Como o Minitab remove preditores fortemente correlacionados da equação de regressão noAjustar modelo linear generalizado
- O Minitab executa uma decomposição QR na matriz X.
Observação
Usar a decomposição QR para calcular R2 é mais rápido que usar regressão de mínimos quadrados.
- O Minitab faz a regressão em todos os outros preditores e calcula o valor R2. Se 1 - R2 < 4 * 2,22e-16, o preditor falha no teste e é removido do modelo.
- O Minitab repete as etapas 1 e 2 para os outros preditores.
Exemplo
- O Minitab faz a regressão de X5 em X1-X4. Se 1 - R2 for maior que 4 * 2,22e-16, X5 permanece na equação. X5 passa no teste e permanece na equação.
- O Minitab faz a regressão de X4 em X1, X2, X3 e X5. Suponha que 1 - R2 para essa regressão é maior que 4 * 2,22e-16 e por isso permanece na equação.
- O Minitab faz a regressão de X3 em X1, X2, X4 e X5 e calcula o valor R2. X3 falha no teste e é removido da equação.
- O Minitab faz uma nova decomposição QR na matriz X e faz a regressão de X2 nos preditores restantes, X1, X4 e X5. X2 passa no teste.
- O Minitab faz a regressão de X1 em X2, X4 e X5. Ele falha no teste e é removido da equação.
O Minitab faz a regressão de Y em X2, X4, X5. Os resultados incluem uma mensagem informando que os preditores X1 e X3 não podem ser estimados e foram removidos do modelo.
Observação
Você pode usar o subcomando TOLERANCE com o comando de sessão REGRESS para forçar o Minitab a manter um preditor altamente correlacionado com outro preditor no modelo. Entretanto, diminuir a tolerância pode ser perigoso, e pode produzir resultados numericamente inexatos.
