Neste tópico
Etapa1: Determine se a associação entre a resposta e o termo é estatisticamente significativa
- Valor-p ≤ α: a associação é estatisticamente significativa
- Se o valor-p for menor ou igual ao nível de significância, é possível concluir que há uma associação estatisticamente significativa entre a variável de resposta e o termo.
- Valor-p > α: a associação não é estatisticamente significativa
- Se o valor-p for maior ou igual ao nível de significância, não é possível concluir que há uma associação estatisticamente significativa entre a variável de resposta e o termo. Talvez seja necessário reajustar o modelo sem o termo.
- Se um fator fixo é significativo, é possível concluir que nem todas as médias de nível são iguais.
- Se um fator aleatório é significativo, é possível concluir que o fator contribui para a quantidade de variação na resposta.
- Se um termo de interação é significativo, a relação entre um fator e a resposta depende dos outros fatores do termo. Neste caso, você não deve interpretar os principais efeitos sem considerar o efeito da interação.
- Se uma covariável for estatisticamente significativa, é possível concluir que as mudanças no valor da covariável estejam associadas a mudanças no valor médio da resposta.
- Se um termo polinomial for significativo, é possível concluir que os dados contêm curvatura.
Coeficientes
| Termo | Coef | EP de Coef | Valor-T | Valor-P | VIF |
|---|---|---|---|---|---|
| Constante | -4969 | 191 | -25,97 | 0,000 | |
| Temperatura | 83,87 | 3,13 | 26,82 | 0,000 | 301,00 |
| TipoVidro | |||||
| 1 | 1323 | 271 | 4,89 | 0,000 | 3604,00 |
| 2 | 1554 | 271 | 5,74 | 0,000 | 3604,00 |
| Temperatura*Temperatura | -0,2852 | 0,0125 | -22,83 | 0,000 | 301,00 |
| Temperatura*TipoVidro | |||||
| 1 | -24,40 | 4,42 | -5,52 | 0,000 | 15451,33 |
| 2 | -27,87 | 4,42 | -6,30 | 0,000 | 15451,33 |
| Temperatura*Temperatura*TipoVidro | |||||
| 1 | 0,1124 | 0,0177 | 6,36 | 0,000 | 4354,00 |
| 2 | 0,1220 | 0,0177 | 6,91 | 0,000 | 4354,00 |
Principais resultados: valor de P, coeficientes
Nestes resultados, os principais efeitos para o tipo e temperatura do vidro são estatisticamente significativos ao nível de significância de 0,05. Você pode concluir que as mudanças nessas variáveis estão associadas às alterações na variável resposta.
Dos três tipos de vidro no experimento, a saída exibe os coeficientes para dois tipos. Por padrão, o Minitab remove um nível de fator para evitar a multicolinearidade perfeita. Como a análise utiliza o esquema de codificação -1, 0, +1, os coeficientes para os efeitos principais representam a diferença entre cada média de nível e média geral. Por exemplo, o tipo de vidro 1 está associado com a saída de luz que é 1323 unidades maior do que a média global.
A temperatura é uma covariável neste modelo. O coeficiente para o efeito principal representa a mudança na resposta média para o aumento da unidade um na covariável, enquanto os outros termos no modelo são mantidos constantes. Para cada aumento de um grau na temperatura, a saída média de luz aumenta em 83,87 unidades.
Tanto o tipo de vidro como a temperatura estão incluídos nos termos de ordem superior que são estatisticamente significativos.
Os termos de interação com dois e três fatores para o tipo e temperatura do vidro são estatisticamente significativos. Estas interações indicam que a relação entre cada uma das variáveis e a resposta depende do valor da outra variável. Por exemplo, o efeito do tipo de vidro na saída de luz depende da temperatura.
O termo polinomial, Temperatura*Temperatura, indica que a curvatura na relação entre a temperatura e a saída de luz é estatisticamente significativa.
Os principais efeitos não devem ser interpretados independentemente dos efeitos de interação e curvatura. Para obter uma melhor compreensão dos efeitos principais, efeitos de interação e curvatura em seu modelo, acesse Gráficos Fatoriais e Otimizador de Resposta.
Etapa 2: Determinar quão bem o modelo se ajusta aos seus dados
Para determinar se o modelo ajusta bem os dados, examine as estatísticas de qualidade do ajuste tabela do resumo do modelo.
- S
-
Use S para avaliar se o modelo descreve bem a resposta. Use S em vez das estatísticas de R2 para comparar o ajuste de modelos que não têm constante.
S é medido nas unidades da variável de resposta e representa o quão longe os valores de dados caem dos valores ajustados. Quanto mais baixo for o valor de S, melhor o modelo descreve a resposta. No entanto, um valor de S baixo por si só não indica que o modelo satisfaz aos pressupostos do modelo. Você deve verificar os gráficos de resíduos para conferir os pressupostos.
- R2
-
Quanto mais alto o valor de R2 melhor o modelo ajusta seus dados. O valor de R2 está sempre entre 0 e 100%.
O R2 sempre aumenta quando você adiciona mais preditores a um modelo. Por exemplo, o melhor modelo de cinco preditores terá sempre um R2 que é pelo menos tão elevado quanto o melhor modelo de quatro preditores. Portanto, R2 é mais útil quando for comparado a modelos do mesmo tamanho.
- R2 (aj)
-
Use o R2 ajustado quando desejar comparar modelos que têm diferentes números de preditores. R2 sempre aumenta quando você adiciona um preditor ao modelo, mesmo quando não existe uma verdadeira melhoria ao modelo. O valor de R2 ajustado incorpora o número de preditores no modelo para ajudá-lo a escolher o modelo correto.
- R2 (pred)
-
Use R2 predito para determinar o quão bem seu modelo prediz as respostas para novas observações.Modelos que têm valores de R2 predito mais elevado têm melhor capacidade preditiva.
Um R2 predito que é substancialmente menor que o R2 pode indicar que o modelo está com excesso de ajuste. Um modelo com excesso de ajuste ocorre quando você adiciona termos para efeitos que não são importantes na população. O modelo se adapta aos dados de amostra e, por conseguinte, pode não ser útil para fazer predições em relação à população.
O R2 previsto também pode ser mais útil do que o R2 ajustado para a comparação de modelos, porque ele é calculado com as observações que não estão incluídas no cálculo do modelo.
- AICc e BIC
- Quando você mostra os detalhes para cada etapa de um método stepwise ou quando você mostra os resultados expandidos da análise, o Minitab mostra mais duas estatísticas. Essas estatísticas são o Critério de Informação de Akaike Corrigido (AICc) e o Critério de Informação Bayesiano (BIC). Use essas estatísticas para comparar modelos diferentes. Para cada estatística, valores menores são preferíveis. O Minitab não exibe estas estatísticas e nem executa métodos stepwise quanto os dados incluem fatores aleatórios.
-
Amostras pequenas não fornecem uma estimativa precisa da força da relação entre a resposta e os preditores. Por exemplo, se você precisar que R2 seja mais exato, deve usar uma amostra maior (geralmente, 40 ou mais).
-
A estatística de qualidade do ajuste é apenas uma medida do grau em que o modelo ajusta os dados (se ajusta bem ou mal). Mesmo quando um modelo tem um um valor desejável, você deve verificar os gráficos de resíduos para conferir se o modelo atende aos pressupostos do modelo.
Sumário do Modelo
| S | R2 | R2(aj) | R2(pred) |
|---|---|---|---|
| 19,1185 | 99,73% | 99,61% | 99,39% |
Principais resultados: S, R2, R2 (aj), R2 (pred)
Nestes resultados, o modelo explica 99,73% da variação na saída de luz das amostras de visores de vidro. Por estes dados, o valor de R2 indica que o modelo fornece um bom ajuste aos dados. Se os modelos adicionais forem ajustados com diferentes preditores, utilize os valores de R2 ajustados e os valores de R2 preditos para comparar se os modelos ajustam bem os dados.
Etapa 3: Determinar se o modelo atende às suposições da análise
Use os gráficos de resíduos para ajudar a determinar se o modelo é adequado e satisfaz aos pressupostos da análise. Se os pressupostos não forem satisfeitos, o modelo pode não ajustar bem os dados e você deve ter cautela ao interpretar os resultados.
Para obter mais informações sobre como lidar com os padrões nos gráficos residuais, vá para Gráficos de resíduos para Ajustar modelo linear generalizado e clique no nome do gráfico residual na lista na parte superior da página.
Gráficos de resíduos versus de ajustes
Use o gráfico de resíduos versus ajustes para verificar a pressuposição de que os resíduos são aleatoriamente distribuídos e têm variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Curvilíneo | Um termo de ordem mais alta ausente |
| Um ponto que está distante de zero | Um outlier |
| Um ponto que é distante dos outros pontos na direção x | Um ponto influente |
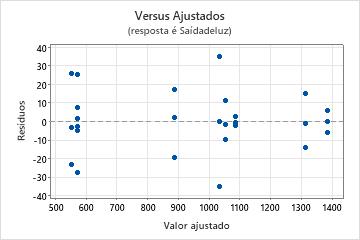
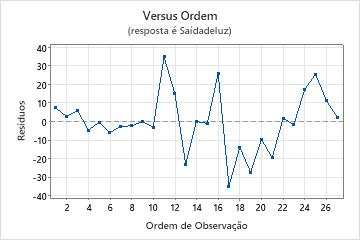
Gráfico de resíduos versus ordem
Tendência
Deslocamento
Ciclo
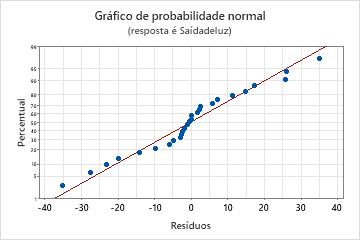
Gráficos de probabilidade normal dos resíduos
Use o gráfico de probabilidade normal de resíduos para verificar a pressuposição de que os resíduos são distribuídos normalmente. O gráfico de probabilidade normal dos resíduos deve seguir aproximadamente uma linha reta.
| Padrão | O que o padrão pode indicar |
|---|---|
| Não é uma linha reta | Não normalidade |
| Um ponto que está distante da linha | Um outlier |
| Alteração de inclinação | Uma variável não identificada |