Neste tópico
- R2 (aj)
- Componentes da variância
- Quadrados médios esperados
- Estatística-f para modelos com fatores aleatórios
- Como as estatísticas F são calculadas na saída da ANOVA
- Por que a saída da ANOVA inclui um "x" ao lado de um valor p na tabela ANOVA e o rótulo "Não é um teste F exato"?
- Sobre a mensagem "Denominador do teste F zero ou não definido"
- valor ajustado
- Resíduos (Resid)
Modelo da ANOVA balanceada
O modelo da ANOVA balanceada por três ou mais fatores é uma extensão direta de um modelo da análise de variância com dois fatores.
Um modelo da ANOVA balanceada com três fatores A, B e C é:
yijkm = μ + α i+ β j + γ k + (αβ)ij+ (αγ)ik+ (βγ)jk+ (αβγ)ijk+εijkm
Se os fatores forem fixos, Σαi = 0, Σβj = 0, Σγk = 0, Σ(αβ)ij = 0, Σ(αγ)ik = 0, Σ(βγ)jk = 0, Σ(αβγ)ijk = 0 e εijkm são independentes N(0, σ2).
Se os fatores forem aleatórios, α i, β j , γk, (αβ)ij, (αγ)ik, (βγ)jk, (αβγ)ijk, e εijkm são variáveis aleatórias independentes. As variáveis são normalmente distribuídas com média zero e variâncias dadas por V(αi) = σ2α,V(β j) = σ2β,V(γk) = σ2γ, V[(αβ)ij] = σ2αβ, V[(αγ)jk] = σ2αγ, V[(βγ)jk] = σ2βγ, V(εijkm) = σ2.
O modelo de três fatores pode ser estendido para modelos com mais de três fatores.
Médias de Fator
Fórmula
A média de observações para um fator a um determinado nível. As fórmulas são:
Média do fator A: 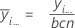
Média do fator B: 
Média do fator C: 
Média global: 
Notação
| Termo | Descrição |
|---|---|
| yi... | soma de todas as observações para o io nível do fator A |
| y.j.. | soma de todas as observações para o jo nível do fator B |
| y..k. | soma de todas as observações para o ko nível do fator C |
| y.... | a soma de todas as observações da amostra |
| a | número de níveis em A |
| b | número de níveis em B |
| c | número de níveis em C |
| n | número de observações em cada combinação de fatores e níveis |
Soma de quadrados (SS)
A soma das distâncias ao quadrado. SS total é a variação total nos dados. SS (A), SS (B) e SS (C) representam a quantidade de variação da média de nível de fator estimado em torno da média global. Eles também são conhecidos como a soma dos quadrados entre tratamentos. SS (AB), SS (AC), SS (BC) e SS (ABC) representam a quantidade de variação explicada por cada termo de interação respectivo. SS Erro representa a quantidade de variação entre o valor ajustado e a observação real. Também é conhecido como erro dentro de tratamentos. Estas fórmulas assumem que um modelo completo está ajustado. Os cálculos são:



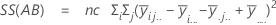
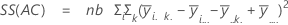
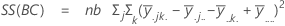
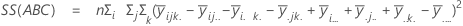
- SS Erro = SS Total - SS (para todos os termos no modelos)
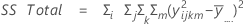
Notação
| Termo | Descrição |
|---|---|
| a | número de níveis no fator A |
| b | número de níveis no fator B |
| c | número de níveis no fator C |
| n | número total de ensaios |
 | média do io nível de fator do fator A |
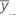 | média global de todas as observações |
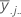 | média do jo nível de fator do fator B |
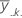 | média do ko nível de fator do fator C |
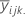 | média de tratamento estimada |
Graus de liberdade (DF)
Os graus de liberdade para cada componente do modelo são:
| Fontes da variação | DF |
|---|---|
| Fator | ki – 1 |
| Covariáveis e interações entre covariáveis | 1 |
| Interações que envolvem fatores | 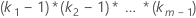 |
| Regressão | p |
| Erro | n – p – 1 |
| Total | n – 1 |
Notação
| Termo | Descrição |
|---|---|
| ki | número de níveis no io fator |
| m | número de fatores |
| n | número de observações |
| p | número de coeficientes no modelo, sem contar com a constante |
Quadrado Médio (MS)
Fórmulas
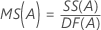
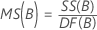
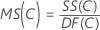
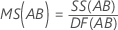
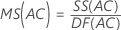
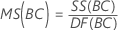
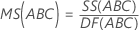
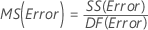
F
Para uma ANOVA com três fatores, sendo que todos são fatores fixos, essas fórmulas são estatísticas F quando o modelo é completo.
Fórmulas

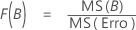


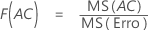
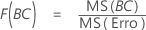
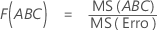
- Para F(A), os graus de liberdade para o numerador são a - 1 e para o denominador são (n - 1)abc.
- Para F(B), os graus de liberdade para o numerador são b - 1 e para o denominador são (n - 1)abc.
- Para F(C), os graus de liberdade para o numerador são c - 1 e para o denominador são (n - 1)abc.
- Para F(AB), os graus de liberdade para o numerador são (a - 1)(b - 1) e para o denominador são (n - 1)abc.
- Para F(AC), os graus de liberdade para o numerador são (a - 1)(c - 1) e para o denominador são (n - 1)abc.
- Para F(BC), os graus de liberdade para o numerador são (a - 1)(c - 1) e para o denominador são (n - 1)abc.
- Para F(ABC), os graus de liberdade para o numerador são (a - 1)(b - 1)(c - 1) e para o denominador são (n - 1)abc.
Se houver fatores aleatórios no modelo, a razão F para cada termo é determinada pelo quadrado médio esperado para cada termo.
Valores maiores de F suportam a rejeição da hipótese nula. É possível concluir que o efeito seja estatisticamente significativo.
Valor-p – Tabela Análise de Variância
O valor-p é a probabilidade que é calculada a partir de uma distribuição-f com graus de liberdade (DF) como a seguir:
- DF do numerador
- soma dos graus de liberdade para o termo ou os termos do teste
- DF do denominador
- graus de liberdade para erro
Fórmula
1 − P(F ≤ fj)
Notação
| Termo | Descrição |
|---|---|
| P(F ≤ f) | função de distribuição acumulada para a distribuição F |
| f | estatística F de teste |
S

Notação
| Termo | Descrição |
|---|---|
| MSE | quadrado médio do erro |
R2
R2 também é conhecido como o coeficiente de determinação.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| yi | i o valor de resposta observada |
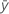 | resposta média |
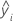 | i a resposta ajustada |
R2 (aj)
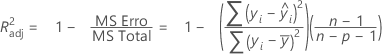
Enquanto os cálculos para R2 ajustado podem produzir valores negativos, o Minitab exibe zero para estes casos.
Notação
| Termo | Descrição |
|---|---|
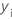 | i o valor de resposta observada |
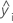 | ia resposta ajustada |
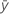 | resposta média |
| n | número de observações |
| p | o número de termos no modelo |
Componentes da variância
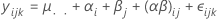
onde, αi, βj , (αβ)ij e εijk são variáveis aleatórias independentes. As variáveis são normalmente distribuídas com média zero e variações destas fórmulas dadas por:
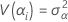

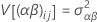

Estas variâncias são os componentes de variância. Neste caso, teste a hipótese de que os componentes de variância são iguais a zero.
Para um modelo restrito misto com dois fatores, o modelo é:
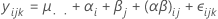
em que αi é um efeito fixo e βj é um efeito aleatório, (αβ)ij, é um efeito aleatório e εijk é um erro aleatório. O Σαi = 0 e o Σ(αβ)ij = 0 para cada j. As variâncias são V(βj) = σ2β,V[(αβ)ij] =[(a - 1)/a]σ2αβ e V(εijk) = σ2. σ2β, σ2αβ e σ2 são componentes de variância. A soma do componente de interação com o fator fixo é igual ao valor zero, o que indica que este é o modelo misto restrito.
Para um modelo misto sem restrições, com um fator fixo, A, e um fator aleatório, B, esta fórmula descreve o modelo:
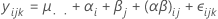
em que αi são efeitos fixos e βj, (αβ)ij e εijk são variáveis aleatórias não correlacionadas com médias zero e estas variâncias:

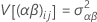

Estas variâncias são os componentes de variância. O Σα i = 0 e o Σ(αβ)ij = 0 para cada j.
Estas informações são para modelos balanceados. Para obter informações sobre modelos não balanceados ou mais complexos, consulte Montgomery1 e Neter2.
- D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Quadrados médios esperados
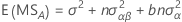



As fórmulas para os quadrados médios esperados para um modelo para um modelo misto restrito com dois fatores, A (fixo) e B (aleatório) são os seguintes:
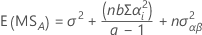



As fórmulas para os quadrados médios esperados para um modelo misto irrestrito com um fator fixo, A, e um fator aleatório, B, são:
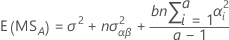



Para as regras gerais sobre o cálculo dos quadrados médios esperados e para obter informações sobre modelos desbalanceados ou mais complexos, consulte Montgomery1 e Neter2.
- D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Notação
| Termo | Descrição |
|---|---|
| b | número de níveis no fator B |
| a | número de níveis no fator A |
| n | número de observações |
| σ2 | variância estimada do modelo |
 | variância estimada de A |
 | variância estimada de B |
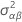 | variância estimada de AB |
 | efeitos fixos de A |
Estatística-f para modelos com fatores aleatórios
Como as estatísticas F são calculadas na saída da ANOVA
Cada estatística F é uma razão de quadrados médios. O numerador é o quadrado médio para o termo. O denominador é escolhido de tal modo que o valor esperado do quadrado médio do numerador difere do valor esperado do quadrado médio do denominador apenas pelo efeito de interesse. O efeito para um termo aleatório é representado pelo componente de variância do termo. O efeito para um termo fixo é representado pela soma dos quadrados dos componentes do modelo associada a esse termo dividida por seus graus de liberdade. Por conseguinte, uma estatística F elevada indica um efeito significativo.
Quando todos os termos do modelo são fixos, o denominador para cada estatística F é o quadrado médio do erro (MSE). No entanto, para modelos que incluem termos aleatórios, o MSE não é sempre o quadrado médio correto. Os quadrados médios esperados (EMS) podem ser utilizados para determinar qual é apropriado para o denominador.
Exemplo
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Tela | (4) + 2.0000(3) + Q[1] |
| (2) Tec | (4) + 2,0000(3) + 4,0000(2) |
| (3) tela * Tec | (4) + 2,0000(3) |
| (4) Erro | (4) |
Um número entre parênteses indica um efeito aleatório associado ao termo relacionado ao lado do número de fonte. (2) representa o efeito aleatório de Tech, (3) representa o efeito aleatório da interação de Screen*Tech, e (4) representa o efeito aleatório de Erro. O EMS para Erro é o efeito do termo de erro. Além disso, o EMS para Screen*Tech é o efeito do termo de erro mais duas vezes o efeito da interação Screen*Tech.
Para calcular a estatística F para Screen*Tech, o quadrado médio para Screen*Tech é dividido pelo quadrado médio do erro, de forma que o valor esperado do numerador (EMS para Screen*Tech = (4) + 2,0000 (3) ) difere do valor esperado do denominador (EMS para o erro = (4)) apenas pelo efeito da interação (2,0000 (3)). Por isso, uma estatística F elevada indica uma interação Screen*Tech significativa.
Um número com Q[ ] indica um efeito fixo associado ao termo relacionado ao lado do número de fonte. Por exemplo, Q[1] é o efeito fixo de Tela. O EMS para Tela é o efeito do termo de erro mais duas vezes o efeito da interação Tela*Tec mais uma constante vezes o efeito da tela. Q[1] é igual a (b*n * (soma ((coeficientes para níveis de Tela)**2)) dividida por (a - 1), em que a e b são o número de níveis de Tela e Tech, respectivamente, e n é o número de replicações.
Para calcular a primeira estatística para Tela * Tec, a média quadrada para Tela * Tec é dividida pela média quadrada do erro de forma que o valor esperado do numerador (EMS para Tela * Tec = (4) + 2,0000(3) + Q[1]) difere do valor esperado do denominador (EMS para Tela * Tec = (4) + 2,0000(3)) somente pelo efeito de Tela Q[1]). Por isso, uma estatística F elevada indica uma interação Screen significativa.
Por que a saída da ANOVA inclui um "x" ao lado de um valor p na tabela ANOVA e o rótulo "Não é um teste F exato"?
Um teste F exato para um termo é um dos quais o valor esperado da média quadrada do numerador difere do valor esperado da média quadrada do denominador apenas pelo componente de variância ou o fator de interesse fixo.
Algumas vezes, porém, não é possível calcular a média quadrada. Nesse caso, o Minitab usa uma média quadrada que resulte em um teste F aproximado e exibe "x" ao lado do valor de p para identificar que o teste F não é exato.
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Suplemento | (4) + 1,7500(3) + Q[1] |
| (2) Lago | (4) + 1,7143(3) + 5,1429(2) |
| (3) Suplemento * Lago | (4) + 1,7500(3) |
| (4) Erro | (4) |
A estatística F para o suplemento é a média quadrada de Suplement dividida pela média quadrada da interação Supplement*Lake. Se o efeito para Suplement for pequeno demais, o valor esperado do numerador é igual ao valor esperado do denominador. Este é um exemplo de um teste F exato.
Observe, no entanto, que, para um efeito pequeno demais de Lake, não existem médias quadradas de forma que o valor esperado do numerador é igual ao valor esperado do denominador. Portanto, o Minitab usa um teste F aproximado. Neste exemplo, a média quadrada de Lake é dividida pela média quadrado para a interação Supplement*Lake. Isto resulta em um valor esperado do numerador aproximadamente igual ao do denominador caso o efeito de Lake seja muito pequeno.
Sobre a mensagem "Denominador do teste F zero ou não definido"
- Não existe pelo menos um grau de liberdade para erro.
-
Os valores de MS ajustados são muito pequenos e, portanto, não há de precisão suficiente para exibir o F e os valoresdep. Como solução, multiplique a coluna de resposta por 10. Em seguida, realize o mesmo modelo de regressão, mas, em vez disso, use esta nova coluna de resposta para a resposta.
Observação
Multiplicar os valores de resposta por 10 não afetará os valores de F e de p que o Minitab exibe na saída. No entanto, a posição decimal será afetada na saída restante, especificamente, as colulas das somas dos quadrados sequenciais, Adj SS, Adj MS, Ajuste, erro padrão dos ajustes e dos resíduos.
Como as estatísticas F são calculadas na saída da ANOVA
Cada estatística F é uma razão de quadrados médios. O numerador é o quadrado médio para o termo. O denominador é escolhido de tal modo que o valor esperado do quadrado médio do numerador difere do valor esperado do quadrado médio do denominador apenas pelo efeito de interesse. O efeito para um termo aleatório é representado pelo componente de variância do termo. O efeito para um termo fixo é representado pela soma dos quadrados dos componentes do modelo associada a esse termo dividida por seus graus de liberdade. Por conseguinte, uma estatística F elevada indica um efeito significativo.
Quando todos os termos do modelo são fixos, o denominador para cada estatística F é o quadrado médio do erro (MSE). No entanto, para modelos que incluem termos aleatórios, o MSE não é sempre o quadrado médio correto. Os quadrados médios esperados (EMS) podem ser utilizados para determinar qual é apropriado para o denominador.
Exemplo
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Tela | (4) + 2.0000(3) + Q[1] |
| (2) Tec | (4) + 2,0000(3) + 4,0000(2) |
| (3) tela * Tec | (4) + 2,0000(3) |
| (4) Erro | (4) |
Um número entre parênteses indica um efeito aleatório associado ao termo relacionado ao lado do número de fonte. (2) representa o efeito aleatório de Tech, (3) representa o efeito aleatório da interação de Screen*Tech, e (4) representa o efeito aleatório de Erro. O EMS para Erro é o efeito do termo de erro. Além disso, o EMS para Screen*Tech é o efeito do termo de erro mais duas vezes o efeito da interação Screen*Tech.
Para calcular a estatística F para Screen*Tech, o quadrado médio para Screen*Tech é dividido pelo quadrado médio do erro, de forma que o valor esperado do numerador (EMS para Screen*Tech = (4) + 2,0000 (3) ) difere do valor esperado do denominador (EMS para o erro = (4)) apenas pelo efeito da interação (2,0000 (3)). Por isso, uma estatística F elevada indica uma interação Screen*Tech significativa.
Um número com Q[ ] indica um efeito fixo associado ao termo relacionado ao lado do número de fonte. Por exemplo, Q[1] é o efeito fixo de Tela. O EMS para Tela é o efeito do termo de erro mais duas vezes o efeito da interação Tela*Tec mais uma constante vezes o efeito da tela. Q[1] é igual a (b*n * (soma ((coeficientes para níveis de Tela)**2)) dividida por (a - 1), em que a e b são o número de níveis de Tela e Tech, respectivamente, e n é o número de replicações.
Para calcular a primeira estatística para Tela * Tec, a média quadrada para Tela * Tec é dividida pela média quadrada do erro de forma que o valor esperado do numerador (EMS para Tela * Tec = (4) + 2,0000(3) + Q[1]) difere do valor esperado do denominador (EMS para Tela * Tec = (4) + 2,0000(3)) somente pelo efeito de Tela Q[1]). Por isso, uma estatística F elevada indica uma interação Screen significativa.
Por que a saída da ANOVA inclui um "x" ao lado de um valor p na tabela ANOVA e o rótulo "Não é um teste F exato"?
Um teste F exato para um termo é um dos quais o valor esperado da média quadrada do numerador difere do valor esperado da média quadrada do denominador apenas pelo componente de variância ou o fator de interesse fixo.
Algumas vezes, porém, não é possível calcular a média quadrada. Nesse caso, o Minitab usa uma média quadrada que resulte em um teste F aproximado e exibe "x" ao lado do valor de p para identificar que o teste F não é exato.
| Fonte | Média Quadrada Esperada para Cada Termo |
|---|---|
| (1) Suplemento | (4) + 1,7500(3) + Q[1] |
| (2) Lago | (4) + 1,7143(3) + 5,1429(2) |
| (3) Suplemento * Lago | (4) + 1,7500(3) |
| (4) Erro | (4) |
A estatística F para o suplemento é a média quadrada de Suplement dividida pela média quadrada da interação Supplement*Lake. Se o efeito para Suplement for pequeno demais, o valor esperado do numerador é igual ao valor esperado do denominador. Este é um exemplo de um teste F exato.
Observe, no entanto, que, para um efeito pequeno demais de Lake, não existem médias quadradas de forma que o valor esperado do numerador é igual ao valor esperado do denominador. Portanto, o Minitab usa um teste F aproximado. Neste exemplo, a média quadrada de Lake é dividida pela média quadrado para a interação Supplement*Lake. Isto resulta em um valor esperado do numerador aproximadamente igual ao do denominador caso o efeito de Lake seja muito pequeno.
Sobre a mensagem "Denominador do teste F zero ou não definido"
- Não existe pelo menos um grau de liberdade para erro.
-
Os valores de MS ajustados são muito pequenos e, portanto, não há de precisão suficiente para exibir o F e os valoresdep. Como solução, multiplique a coluna de resposta por 10. Em seguida, realize o mesmo modelo de regressão, mas, em vez disso, use esta nova coluna de resposta para a resposta.
Observação
Multiplicar os valores de resposta por 10 não afetará os valores de F e de p que o Minitab exibe na saída. No entanto, a posição decimal será afetada na saída restante, especificamente, as colulas das somas dos quadrados sequenciais, Adj SS, Adj MS, Ajuste, erro padrão dos ajustes e dos resíduos.
valor ajustado
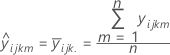
Notação
Para um modelo com três fatores:
| Termo | Descrição |
|---|---|
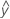 | o valor ajustado para a observação no io nível do fator A, o jo nível do fator B, o ko nível do fator C |
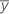 | o valor médio para a observação no io nível do fator A, o jo nível do fator B, o ko nível do fator C |
| n | o número de observações no io nível do fator A, o jo nível do fator B, o ko nível do fator C |
Resíduos (Resid)
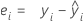
Notação
| Termo | Descrição |
|---|---|
| ei | i o resíduo |
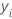 | i o valor de resposta observada |
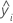 | i a resposta ajustada |
