Neste tópico
Método
Para modelos com dois fatores, a análise das médias é um procedimento para determinar se os efeitos de interação são significativos ou os principais efeitos são diferentes da média global. Para a análise de médias com dois fatores, os dados devem ser balanceados.
Média
Fórmula
A média de observações para um fator a um determinado nível. O Minitab representa graficamente a média para cada nível de fator no gráfico.
| Média do fator A ao io nível: |
 |
| Média do fator B ao jo nível: |
 |
Notação
| Termo | Descrição |
|---|---|
| yi. | soma de todas as observações para o io nível do fator A |
| y.j. | soma de todas as observações para o jo nível do fator B |
| a | número de níveis em A |
| b | número de níveis em B |
| n | número de casos no io nível de fator A e o jo nível de fator B |
Média Global (linha central)
Fórmula
A média de todas as observações da amostra. O Minitab utiliza a média global como a linha central no gráfico dos efeitos principais.

Notação
| Termo | Descrição |
|---|---|
| y... | a soma de todas as observações da amostra |
| a | número de níveis em A |
| b | número de níveis em B |
| n | número de casos no io nível de fator A e o jo nível de fator B |
Limites de decisão superior e inferior para efeitos principais
Os limites de decisão indicam se as médias de nível fator são diferentes da média global. Os pontos que estiverem fora do limite de decisão superior (UDL) ou do limite de decisão inferior (LDL) são estatisticamente diferentes da média global.
O cálculo dos limites de decisão superior e inferior varia com base no número de níveis no fator e no número de observações em cada nível. As fórmulas abaixo mostram os limites de decisão superior e inferior para o fator A. Para calcular os limites de decisão para o fator B, substitua os termos específicos para o fator A pelos termos equivalentes para o fator B.
Fator de dois níveis
Os limites de decisão superior e inferior para o fator A são:
- UDLA =
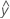 ...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)] - LDLA =
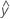 ...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
em que ha = valor absoluto(t(a / 2; abn - ab), MSE = erro médio quadrado (de uma ANOVA com termos A, B e AB) e n1= número de observações em cada nível do fator A.
Fator com mais do que dois níveis
- UDLA =
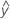 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
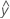 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
em que MSE = erro médio quadrado (de uma ANOVA com termos A, B e AB), a = número de níveis de fator em fator A, e n1= número de observações em cada nível do fator. O valor crítico hα depende do alfa, do número das médias que são representadas graficamente, e dos graus de liberdade para o MSE. Você pode encontrar valores para hα na Tabela B.1 no Apêndice B em Nelson1.
Para valores de alfa fora da faixa de 0,001 e 0,1, os limites de decisão são:
- UDLA =
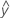 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
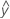 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
em que MSE = erro médio quadrado (de uma ANOVA com termos A, B e AB), n1= número de observações em cada nível do fator hα = valor absoluto (t(α2, df); em que(1- (1- a )** (1 / a)) / 2 e df = nT - ab, em que nT = número total de observações na amostra.
- L.S. Nelson (1983). "Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
Limites de decisão superior e inferior para efeitos principais
Os limites de decisão indicam se a interação é significativa. Os pontos que estiverem fora do limite de decisão superior (UDL) ou limite de decisão inferior (LDL) indicam que a interação é estatisticamente significativa.
Apresentamos abaixo as fórmulas gerais para os limites de decisão superiores e inferiores para a interação de fatores A e B. Os termos são definidos de maneira diferente em função do número de níveis e observações em cada fator.
- UDLAB = hα* Sqrt[MSE * (q / (a * b * n)]
- LDLAB = –hα* Sqrt[MSE * (q / (a * b * n)]
em que ha = valor absoluto (t(α2, dfe)), a = número de níveis no fator A, b = número de níveis no fator B, n = número de observações para cada interação entre fatores, q = graus de liberdade para os efeitos de interação, (a - 1)(b - 1) e dfe = graus de liberdade para erro, o abn - ab.
Os fatores A e B têm ambos dois níveis
- α2 = a / 2
O fator A tem dois níveis e o fator B tem mais de dois níveis
- α2 = (1- (1- a )** (1 / b)) / 2
em que a = número de níveis no fator A e b = número de níveis do fator B.
O fator A tem mais de dois níveis e fator B tem dois níveis
- α2 = (1- (1- a )** (1 / a)) / 2
em que a = número de níveis no fator A e b = número de níveis do fator B.
Os fatores A e B têm mais de dois níveis
- α2 = (1- (1- a )** (1 /a * b)) / 2
em que a = número de níveis no fator A e b = número de níveis do fator B.
