Neste tópico
Método
A análise de médias é um procedimento para determinar se as médias de nível de fator individual são diferentes da média global (média de todas as observações em um fator). Apresentamos abaixo as etapas que o Minitab usa para calcular os resultados da ANOM para um modelo com um fator:
- Calcula a média em cada nível do fator, y̅i. (i = 1, …, r).
- Calcula a média global de todas as observações, y….
- Calcula sp, uma estimativa do desvio padrão de observação.
- Determina o valor hα, que é o valor correspondente ao nível de significância escolhido para o teste e é utilizado nas linhas de decisão superiores e inferiores.
- Calcula os limites de decisão superior e inferior (UDL e LDL).
- Representa graficamente as médias de cada nível de fator com as linhas de referência superior e inferior, e a linha central na média global.
Média
Fórmula
A média de observações de cada nível de fator. O Minitab representa graficamente a média para cada nível de fator no gráfico.
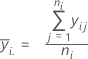
Notação
| Termo | Descrição |
|---|---|
| ni | número de observações no nível de fator i |
| yij | valor da ja observação no io nível de fator |
Média Global (linha central)
Fórmula
A média de todas as observações em todos os níveis de fator. O Minitab utiliza a média global como a linha central no gráfico.
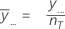
Notação
| Termo | Descrição |
|---|---|
| y... | a soma de todas as observações da amostra |
| nT | número de observações total |
Desvio padrão (StDev)
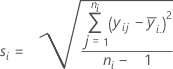
Notação
| Termo | Descrição |
|---|---|
| yij | observações no io nível de fator |
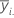 | média de observações no io nível de fator |
| ni | número de observações no io nível de fator |
Desvio padrão combinado
Uma estimativa da variação em todos os níveis de fator. O desvio padrão combinado é usado para calcular os limites de decisão.
Fórmula
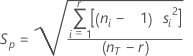
Notação
| Termo | Descrição |
|---|---|
| r | número de níveis |
| nT | número de observações total |
Limites de decisão superior e inferior
Os limites de decisão indicam se as médias de nível fator são diferentes da média global. Os pontos que estiverem fora do limite de decisão superior (UDL) ou do limite de decisão inferior (LDL) são estatisticamente diferentes da média global.
O cálculo dos limites de decisão superior e inferior varia com base no número de níveis no fator e no número de observações em cada nível.
Fator de dois níveis com um número de observações igual a cada nível
- UDL = y.. + hα sp* Sqrt(1/ nT)
- LDL = y.. - hα sp* Sqrt(1/ nT)
onde hα = valor absoluto (t(a / 2, nT - 2)), sp = desvio padrão combinado, e nT = número total de observações.
Fator com mais de 2 níveis, com número igual de observações em cada nível
- UDL = y.. + hα sp* Sqrt[(r-1) / (rn1)]
- LDL = y.. - hα sp* Sqrt[(r-1) / (rn1)]
onde r = número de níveis no fator e n1 = número de observações em cada nível.
Os graus de liberdade são (n1- 1) * r.
Para valores de alfa fora da do intervalo de 0,001 e 0,1, os limites de decisão são:
- UDL = y.. + hα sp* Sqrt[(nT - n1) / (nT* n1)]
- LDL = y.. - hα sp* Sqrt[(nT - n1) / (nT* n1)]
onde hα = valor absoluto (t(α2, df) e α2 = (1- (1- a )** (1 / r)) / 2 e df = nT - r.
Para obter o hα para valores de α entre 0,001 e 0,1, consulte Nelson1.
Fator com mais de 2 níveis, com número diferente de observações em cada nível
- UDLi = y.. + hα sp* Sqrt[(nT - ni) / (nT* ni)]
- LDLi = y.. - hα sp* Sqrt[(nT - ni) / (nT* ni)]
- L.S. Nelson (1983). "Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
