menu

Suporte ao Minitab®

Cálculos para as estatísticas de processos e valores de capacidade para Relatório do processo

O Minitab calcula as estatísticas de processos e valores de capacidade, como mostrado abaixo.

Neste tópico

Constantes não viciadas para estimar desvio padrão de longo prazo e de curto prazo
Desvios padrão de curto prazo
Desvios padrão de longo prazo
Média do processo de longo prazo
Desvio padrão do processo de longo prazo
Média do processo de curto prazo
Desvio padrão do processo de curto prazo
Estatística de capacidade
Graus de liberdade
Probabilidades
Estatísticas de Z.bench

Constantes não viciadas para estimar desvio padrão de longo prazo e de curto prazo

Constantes não viciadas para estimar desvio padrão de longo prazo
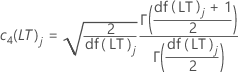
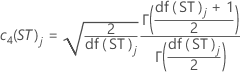
Constantes não viciadas para estimar desvio padrão de curto prazo

onde:

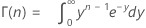
Notação

Termo	Descrição
c₄(LT)_j	Constante não viciada para cálculos de longo prazo no j^o subgrupo acumulado
c₄(ST)_j	Constante não viciada para cálculos de curto prazo no j^o subgrupo acumulado
df(LT)_j	Graus de liberdade de longo prazo no j^o subgrupo
df(ST)_j	Graus de liberdade de curto prazo no j^o subgrupo

Desvios padrão de curto prazo

Desvio padrão de curto prazo com constante não viciada (padrão)
Desvio padrão de curto prazo sem constante não viciada

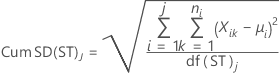
onde:

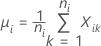
Notação

Termo	Descrição
Cum SD(ST)_j	Desvio padrão de curto prazo acumulado até o j^o subgrupo
c₄(ST)_j	Constante não viciada para cálculos de curto prazo no j^o subgrupo acumulado
df(ST)_j	Graus de liberdade de curto prazo no j^o subgrupo

Desvios padrão de longo prazo

Desvio padrão de longo prazo sem constante não viciada (padrão)
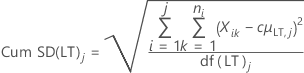
Desvio padrão de longo prazo com constante não viciada

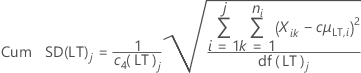
onde:

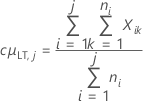
Notação

Termo	Descrição
Cum SD(LT)_j	Desvio padrão de longo prazo acumulado até o j^o subgrupo
c₄(LT)_j	Constante não viciada para cálculos de longo prazo no j^o subgrupo acumulado
df(LT)_j	Graus de liberdade de longo prazo no j^o subgrupo

Média do processo de longo prazo

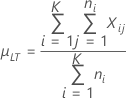
Notação

Termo	Descrição
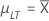
µ_LT	Média de longo prazo ou média do processo μ_LT = cμ_LT,K Observação

Desvio padrão do processo de longo prazo

σ_LT = Cum SD(LT)_K

Média do processo de curto prazo

Se for dado um alvo: μ_ST = T
Se ambas as especificações forem dadas (sem alvo)
Se uma especificação for dada (sem alvo): μ_ST = μ_LT

Notação

Termo	Descrição
µ_ST	Média de curto prazo
T	Alvo
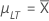
µ_LT	Média de longo prazo ou média do processo Observação

Desvio padrão do processo de curto prazo

σ_ST = Cum SD(ST)_K

Para obter mais informações, vá para Como o Minitab escolhe valores de centralização para as estatísticas de curto prazo para Relatório do processo.

Estatística de capacidade

CCpk
Cp
Cpk
CPL
CPU

Observação

Cp, Cpk e CCpk representam a capacidade potencial do processo. Portanto, estas fórmulas utilizam variabilidade de curto prazo.

Pp
Ppk
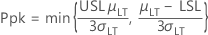
PPL
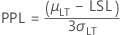
PPU

Observação

Pp e Ppk representam o desempenho real do processo. Portanto, estas fórmulas utilizam variabilidade de longo prazo.

Graus de liberdade

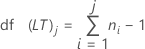
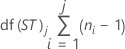
Notação

Termo	Descrição
df(LT)_j	Graus de liberdade de longo prazo no j^o subgrupo
df(ST)_j	Graus de liberdade de curto prazo no j^o subgrupo

Probabilidades

P.LSL(LT)_j

A probabilidade de longo prazo menor ou igual à especificação inferior no j^o subgrupo

P.LSL(LT) _j = 1 – Φ(Z.LSL(LT)_j)

P.LSL(ST) _j

A probabilidade de curto prazo menor ou igual à especificação inferior no j^o subgrupo

P.LSL(ST) _j = 1 – Φ(Z.LSL(ST)_j)

P.USL(LT) _j

A probabilidade de longo prazo maior ou igual à especificação superior no j^o subgrupo

P.USL(LT) _j = 1 – Φ(Z.USL(LT)_j)

P.USL(ST) _j

A probabilidade de curto prazo maior ou igual à especificação superior no j^o subgrupo

P.USL(ST) _j = 1 – Φ(Z.LSL(ST)_j)

P.Total(LT) _j

Total (longo prazo) probabilidade de estar fora da especificação no j^o subgrupo

P.Total(LT) _j = P.USL(LT)_j + P.LSL(LT)_j

P.Total(ST)_j

Total (curto prazo) probabilidade de estar fora da especificação no j^o subgrupo

P.Total(ST)_j = P.USL(ST)_j + P.LSL(ST)_j

Estatísticas de Z.bench

Z.Bench(LT)_j

Benchmark Z (longo prazo) em j^o subgrupo

Z.Bench(LT)_j = Φ⁻¹(P.Total(LT)_j)

Z.Bench(ST)_j

Benchmark Z (curto prazo) em j^o subgrupo

Z.Bench(ST)_j = Φ⁻¹(P.Total(ST)_j)

Z.LSL(LT)_j

Valor de z (longo prazo) para uma especificação inferior no j^o subgrupo

Z.LSL(LT)_j = (μ_LT – LSL) / Cum SD(LT)_j

Z.LSL(ST)_j

Valor de z (curto prazo) para uma especificação inferior no j^o subgrupo

Z.LSL(ST)_j = (μ_ST – LSL) / Cum SD(ST)_j

Z.USL(LT)_j

Valor de z (longo prazo) para uma especificação superior no j^o subgrupo

Z.USL(LT)_j = (USL – μ_LT) / Cum SD(LT)_j

Z.USL(ST)_j

Valor de z (curto prazo) para uma especificação superior no j^o subgrupo

Z.USL(ST)_j = (USL – μ_ST) / Cum SD(ST)_j

Z.Shift_j

Fator de deslocamento no j^o subgrupo

Z.Shift_j = Z.Bench(ST)_j – Z.Bench(LT)_j

Copyright © 2024 Minitab, LLC. All rights Reserved.