Todos os relatórios de capacidade do processo para Relatório do processo

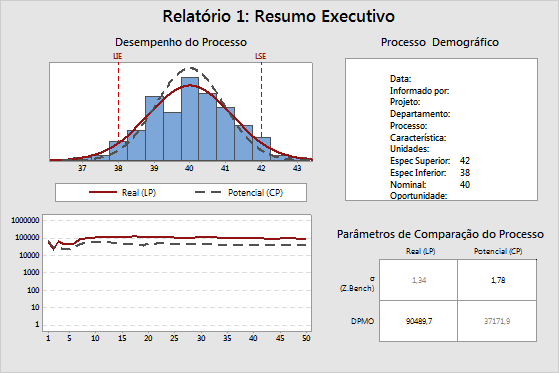
Gráfico superior de desempenho de processo: desempenho de processo estático LT/ST

As curvas normais no histograma apresentam a distribuição estimada das medições dos CTQs do projeto. O CTQ (essencial para a qualidade) refere-se às principais características mensuráveis de um produto ou processo cujos padrões de desempenho devem ser cumpridas a fim de satisfazer o cliente. Os CTQs podem incluir qualquer variável que esteja relacionada ao produto ou serviço e que possa ter os limites de especificação superior e inferior.

O Minitab calcula as curvas a partir das de estimativas de longo prazo (LT) e de curto prazo (ST) da média do processo e do desvio padrão do processo. O Minitab, então, traça uma curva LT normal e uma curva ST normal. Em quase todos os casos, a curva LT normal é mais ampla do que a curva ST normal.

Os limites de especificação (LSL e USL) fornecem pontos de referência. Em geral, mas nem sempre, o valor alvo (valor nominal) está centralizado entre os limites de especificação inferior e superior. De maneira ideal, a média deve estar próxima do valor alvo. No exemplo acima, a média do processo parece estar muito próxima do valor alvo.

Gráfico inferior de desempenho de processo: desempenho de processo dinâmico LT/ST

Este gráfico apresenta o DPMO (defeitos por milhão de oportunidades) estimado acumulado após cada subgrupo de dados, tanto para LT (longo prazo) como para ST (curto prazo). O Minitab calcula o DPMO obtendo primeiro um Z.Bench depois de cada subgrupo e, em seguida, converte-o em um DPMO. Os valores de Z.Bench são funções da média estimada e do desvio padrão, tanto para LT e ST.

Se o processo estiver estável, as linhas neste gráfico se aproximam de um valor constante. Se as linhas não estão se estabilizando, o processo não está estável ou não há dados suficientes. No exemplo acima, ambas as linhas tendem a flutuar no lado esquerdo do gráfico, mas, em seguida, elas estabilizam no lado direito do gráfico. Se as linhas estavam relativamente planas no lado esquerdo do gráfico, elas aumentam ou diminuem de forma constante. Isso indica que alguma coisa no processo pode ter mudado: ou a média mudou, ou em que houve uma mudança na variação do processo. Em quase todos os casos, a linha de LT está acima da linha ST, porque o Z.Bench de LT é menor do que o Z.Bench de ST, devido à influência do processo de desvios e deslocamentos.

Ambas as linhas neste gráfico devem oscilar para cima e para baixo no lado esquerdo, onde há alguns subgrupos, mas devem estabilizar no lado direito caso tenham sido coletados dados suficientes e o processo esteja estável. Se as linhas não estabilizarem, os gráficos no relatório 4, Estatística Acumulada, devem ajudar a determinar se o problema está na insuficiência de dados ou na instabilidade do processo.

Demografia do processo

A tabela demográfica mostra as informações do projeto e do processo especificadas por você.

Benchmarks do processo

Os números em negrito são Sigma (ou Z.Bench) de ST e DPMO de LT. A maioria dos Black Belts relatam o desempenho do processo utilizando estes dois valores.

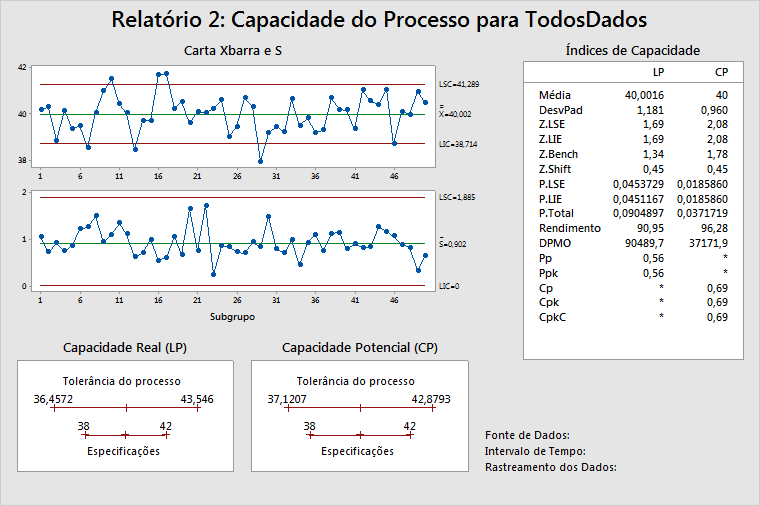
Cartas de controle dos dados do processo

Apresenta a estabilidade do processo ao longo do tempo em que os dados foram coletados. Para subgrupos maiores do que 1, use uma carta Xbarra para ajudar a determinar a estabilidade da média do processo e uma carta S para ajudar a determinar a estabilidade do desvio padrão do processo. Se o tamanho do subgrupo = 1, o Minitab exibe uma carta I com uma carta AM.

Gráficos de capacidade LT/ST

Exibe a tolerância estimada do processo em relação aos limites de especificação. A tolerância do processo é o ponto processo de centralização ± 3 desvios padrão. Existem dois gráficos porque o ponto de centralização do processo e o desvio padrão do processo são diferentes para LT e ST. LT utiliza a média do processo como ponto de centralização, enquanto ST usa o alvo (ou ponto médio entre as especificações, ou a média do processo, quando apenas uma especificação é dada) como ponto de centralização. Consulte Como o Minitab escolhe valores de centralização para as estatísticas de curto prazo para Relatório do processo para obter mais informações.

Em outras palavras, esses gráficos mostram se um carro (o processo) vai caber em uma garagem (as especificações), ou se, para esse assunto, o carro ainda é destinado à garagem. No exemplo acima, o processo é mais amplo do que as especificações. No entanto, o processo está centralizado, como ilustrado no gráfico LT, o que mostra que o ponto de centralização do processo (média) como quase igual ao alvo.

Índices de capacidade LT/ST

Exibe as estatísticas comumente usadas para informar sobre o desempenho do processo. Consulte Compreensão das medidas de capacidade para obter informações sobre uma discussão que compara as estatísticas de medição de longo prazo (LT) e desempenho de curto prazo (ST).

Use os valores Z.Bench para descrever o desempenho do processo. As estatísticas de Z.Bench não apenas são baseadas nas condições de processo apropriadas, mas também levam diretamente a estimativas de probabilidade de um defeito: PPM, DPMO, e assim por diante. As alternativas aceitáveis são CCpk e Ppk, porque elas são baseados nas mesmas condições de processo que as estatísticas de Z.Bench.

Para obter mais informações sobre cálculos específicos, acesse Cálculos para as estatísticas de processos e valores de capacidade para Relatório do processo.

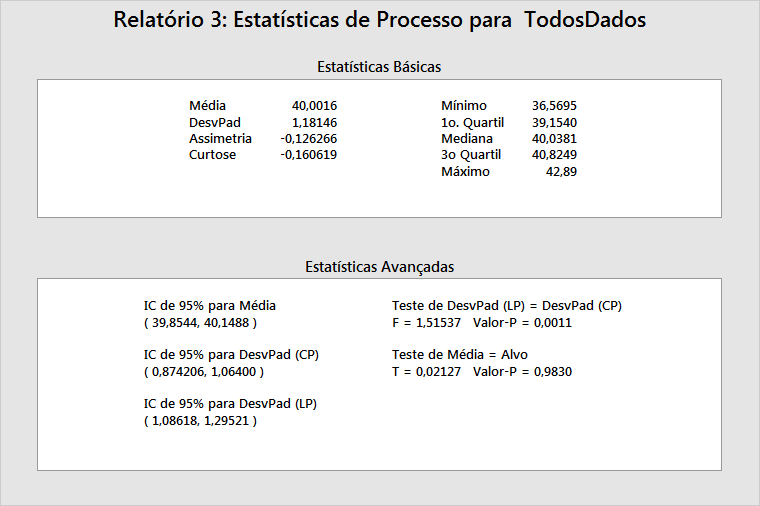
Estatística Básica

Esta tabela fornece a média do processo (média de LT), o desvio padrão do processo (desvio padrão de LT), e outras estatísticas básicas.

Use assimetria e curtose para ajudar a determinar se os dados são normalmente distribuídos. No entanto, os gráficos de probabilidade são muito mais úteis. (No Relatório 6, o Relatório Normal estima a probabilidade de um defeito.)

O mínimo, 1^o quartil, média, 3^o quartil e máximo mostram a dispersão dos dados. Por exemplo, 25% dos dados não são maiores do que 39,154 (1^o quartil), 50% dos dados não são maiores do que 40,0381 (mediana), e 75% dos dados não são maiores do que 40,8249 (3^o quartil).

Estatística Avançada

Esta tabela proporciona inferências estatísticas para os parâmetros do processo, a média de ST e o desvio padrão.

A média do processo inclui um intervalo de confiança de 95% e as estatísticas de teste para mostrar se a média do processo é igual ao alvo do processo. Se a média do processo e o alvo do processo não têm nenhuma diferença estatisticamente significativa, o valor de p será > 0,05, e o alvo do processo estará dentro dos limites do intervalo de confiança. No exemplo acima, o teste tem um valor de p de 0,983 e o alvo (40) se encontra dentro dos limites do intervalo de confiança de 95% para a média. Não é possível rejeitar a hipótese nula de que a média do processo é igual ao alvo do processo.

A tabela também fornece intervalos de confiança de 95% para ambos os desvios padrão de LT e de ST, e um teste para saber se estas duas quantidades são iguais. Caso não exista uma diferença estatisticamente significativa entre os desvios padrão do processo de LT e de ST, é possível concluir que o processo não apresenta deslocamentos e/ou desvios significativos e que não havia causas especiais presentes quando os dados foram coletados. No exemplo acima, o teste de igualdade de variâncias tem um valor de p de 0,0011. Assim, você deve rejeitar a hipótese nula, e concluir que o desvio padrão de LT e o desvio padrão de ST são significativamente diferentes.

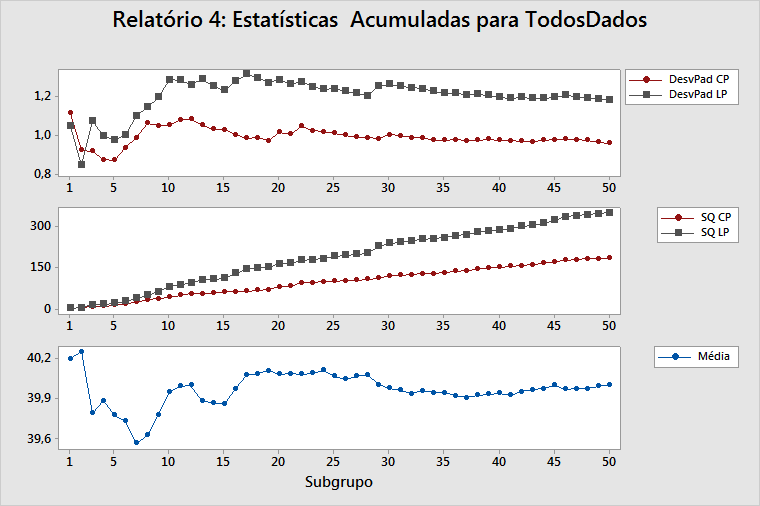
LT/ST de StDev acumuladas

Este gráfico apresenta as estimativas do desvio padrão LT e do desvio padrão de ST após cada subgrupo de dados. Como todas as medidas de desempenho do processo são baseadas nas estimativas do desvio padrão do processo, você deve determinar se estas estimativas são adequadas. Essa adequação depende da existência de um processo estável (um processo em que a variabilidade inerente não está mudando) e de dados suficientes para caracterizar o processo de forma adequada.

As estimativas do desvio padrão de LT e o desvio padrão de ST devem oscilar consideravelmente no lado esquerdo do gráfico, que contém alguns subgrupos. Se o processo estiver estável e você coletou dados suficientes, as estimativas se estabilizarão no lado direito do gráfico. Se as linhas do gráfico continuarem a oscilar, significa que você não coletou dados suficientes ou a variação do processo está instável.

Para um processo estável, o salto entre o desvio padrão de LT e o desvio padrão de ST deve tornar-se razoavelmente constante. Se o processo muda, como um deslocamento na média ou uma mudança na variação, o salto entre o desvio padrão de LT e o desvio padrão de ST também muda.

Para obter mais informações, acesse Identificação dos deslocamentos da média do processo com Relatório do processo, e Identificação de um aumento na variabilidade do processo com Relatório do processo.

LT/ST de SS acumulado

Este gráfico apresenta o desvio da soma dos quadrados (Total de SS ou LT de SS) após cada subgrupo de dados e os desvios da soma de todos os quadrados dentro de cada subgrupo (SS Dentro ou ST de SS) após cada subgrupo de dados. Para obter mais informações, vá para Cálculos para a soma dos quadrados para Relatório do processo.

ST de SS é uma ferramenta de diagnóstico muito boa para a detecção de alterações na variação inerente a um processo. Se a variação inerente estiver estável, a SS Dentro de cada subgrupo será aproximadamente a mesma. Assim, a ST de SS deve aumentar em aproximadamente a mesma quantidade para cada subgrupo, o que resulta em uma linha de ST de SS que tem uma inclinação ascendente constante. Qualquer alteração na variabilidade inerente ao processo é apresentada como uma alteração da inclinação da linha de ST de SS.

O Total de SS é a soma das SS Dentro e SS Entre. Assim, Total de SS é afetado pela estabilidade da variância processo e da média do processo. Se ambos forem estáveis, a contribuição para o SS total será aproximadamente a mesma para cada subgrupo. Assim, a LT de SS deve aumentar em aproximadamente a mesma quantidade para cada subgrupo, o que resulta em uma linha de LT de SS que tem uma inclinação ascendente constante. Qualquer alteração na variabilidade inerente ao processo é apresentada como uma alteração da inclinação da linha de LT de SS.

A mudança repentina na variabilidade do processo inerente afeta tanto a SS Dentro quanto a SS Entre e muda as inclinações de ambas as linhas ST de SS e LT de SS. Assim, uma mudança na inclinação para ambas as linhas indica uma alteração na variabilidade do processo inerente.

O deslocamento da média do processo afeta a SS Entre, mas não a SS Dentro, e altera a inclinação da linha de LT de SS mas não da linha de ST de SS. Assim, uma alteração na inclinação da linha de LT de SS, juntamente com uma alteração nula na inclinação da linha ST de SS, indica uma mudança na média do processo.

Para obter mais informações, acesse Identificação dos deslocamentos da média do processo com Relatório do processo, e Identificação de um aumento na variabilidade do processo com Relatório do processo.

Média acumulada

Este gráfico mostra a estimativa da média do processo depois de cada subgrupo. A adequação da estimativa da média processo depende da quantidade de dados coletados e a estabilidade do processo.

As estimativas devem oscilar para cima e para baixo consideravelmente no lado esquerdo do gráfico, que contém alguns subgrupos. Se o processo estiver estável e você coletou dados suficientes, as estimativas se estabilizarão no lado direito do gráfico. Se as linhas continuam a oscilar, há duas opções: você não coletou dados suficientes ou a média do processo está desviando drasticamente. Observe o gráfico de StDev acumulado para determinar se o problema é que você não tem dados suficientes. Se você não tiver dados suficientes, então as linhas LT e ST também oscilarão.

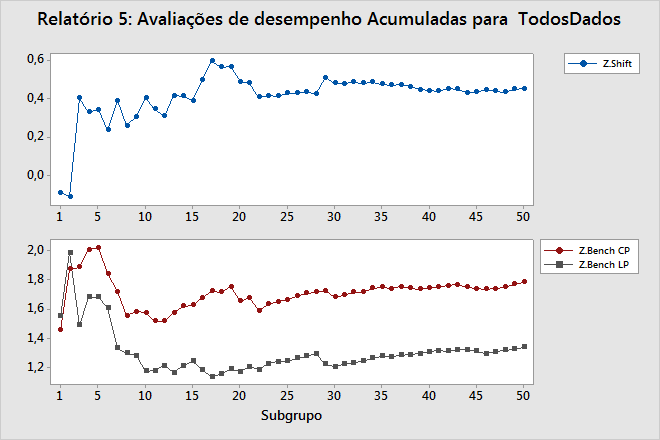
Z.Shift

Z.Shift é igual ao salto entre LT de Z.Bench e ST de Z.Bench.

A linha neste gráfico devem oscilar para cima e para baixo no lado esquerdo, que contém alguns subgrupos, mas devem estabilizar no lado direito caso tenham sido coletados dados suficientes e o processo esteja estável.

LT de Z.Bench e ST e Z.Bench

O gráfico Z.Bench indica se você coletou dados suficientes para utilizar com segurança estas estatísticas a fim de relatar o desempenho do processo. Ambas as linhas neste gráfico devem oscilar para cima e para baixo no lado esquerdo, que contém alguns subgrupos, mas devem estabilizar no lado direito caso tenham sido coletados dados suficientes e o processo esteja estável. Se as linhas não estabilizarem, os gráficos no relatório Estatística Acumulada podem ajudar a determinar se o problema está na insuficiência de dados ou na instabilidade do processo.

Tanto salto no gráfico Z.Bench como a linha no gráfico Z.Shift devem se aproximar de um valor constante, como acontece no exemplo acima.

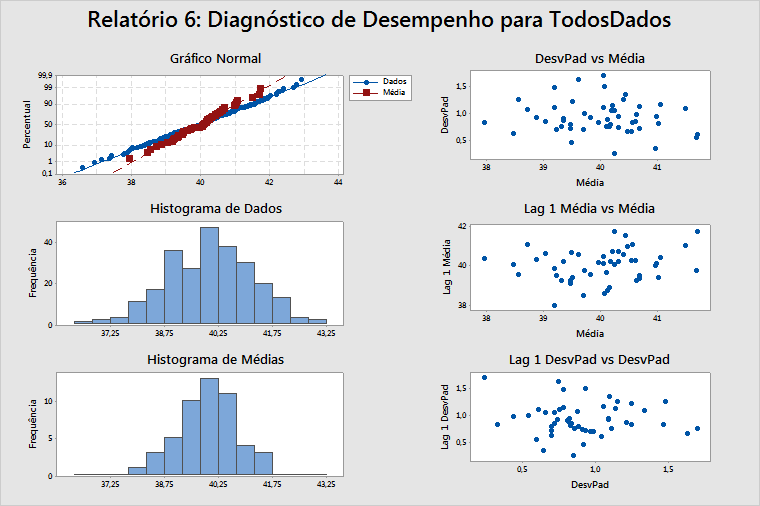
Gráfico normal, Histograma de dados e Histograma de médias

Estes gráficos ajudam a determinar se seus dados são normais. Se os dados forem não normais, as estimativas da probabilidade de ocorrência de um defeito (como DPMO) não serão precisas. Na maioria dos casos, estas estimativas tendem a ser inferiores aos valores reais. Portanto, verifique os gráficos normais e os dois histogramas para ver se os dados são pelo menos razoavelmente normais antes de usar quaisquer estimativas como DPMO. Os dados no exemplo acima parecem ser distribuídos normalmente.

Se os dados parecem ser pouco assimétricos, tente uma transformação como a transformação de Box-Cox, para corrigir o problema. Quando você escolhe Usar transformação de poder de Box-Cox (W = Y^λ) com na subcaixa de diálogo Relatório do processo Opções, o Minitab transforma automaticamente os dados, o alvo e os limites de especificação. No entanto, se você transformar manualmente os dados, é necessário também transformar manualmente o alvo e os limites de especificação.

StDev versus Média

Quando não há nenhuma correlação entre as médias de subgrupo e os desvios padrão subgrupo presente, este gráfico deve apresentar pontos aleatoriamente dispersos, como no exemplo acima.

Caso esteja presente uma correlação positiva entre as médias e os desvios padrão, os desvios padrão do subgrupo tendem a aumentar à medida que as médias do subgrupo aumentam. A transformação de Box-Cox (λ = 0) é uma transformação de estabilização de variância bem conhecida que normalmente funciona bem nesses casos.

Média do Lag 1 vesus Média

Média do Lag 1 versus Média é um gráfico de (a média para o subgrupo)_i versus (a média para o subgrupo)_i–1. Este gráfico deve apresentar pontos dispersos aleatoriamente, como no exemplo acima, o que indica que não há nenhuma correlação entre médias de subgrupo sucessivas presente.

Se houver uma correlação positiva presente e uma média de subgrupo for maior do que a média de processo global, a próxima média de subgrupo também tende a ser maior do que a média de processo geral. Assim, uma correlação positiva implica que o processo está sujeito ao desvio na média. Se a correlação for negativa, isto indica alternância das médias do subgrupo (baixo, em seguida alta, em seguida baixa) e não duas médias baixas consecutivas. Essa correlação negativa implica o controle do processo.

StDev do Lag 1 versus StDev

StDev do Lag 1 versus StDev é um gráfico de (o desvio padrão para o subgrupo)_i versus (o desvio padrão para o subgrupo)_i–1. Este gráfico deve apresentar pontos dispersos aleatoriamente, como no exemplo acima, para mostrar que não há nenhuma correlação entre os desvios padrão sucessivos do subgrupo.

Tal como acontece com as médias de subgrupo, se uma correlação positiva estiver presente e o desvio padrão para um subgrupo for maior do que o desvio padrão da média para todos os subgrupos, o desvio padrão para o próximo subgrupo muito provavelmente também será mais elevado do que o desvio padrão da média para todos os subgrupos. Assim, os desvios padrão do subgrupo tendem a desvios para cima e para baixo. Esta condição pode ser acompanhada por médias que também estão desviando para cima e para baixo, e pela correlação entre as médias de subgrupo e desvios padrão de subgrupo. Neste caso, tente usar uma transformação de Box-Cox com λ = 0.

A autocorrelação positiva nos desvios padrão de subgrupo pode ser causada por desgaste de ferramenta ou outra degradação no processo (o que resulta em uma variação cada vez maior) ou na presença de um fator de perturbação não controlada (como umidade relativa) que afeta a variação.