Neste tópico
Métodos do Intervalo de tolerância
O Minitab calcula intervalos de tolerância paramétricos e não paramétricos. Os cálculos para os intervalos de tolerância paramétricos pressupõem que a distribuição da origem de amostra é normalmente distribuída. Os cálculos para os intervalos de tolerância não paramétricos pressupõem apenas que a distribuição da origem seja contínua.
Definições gerais
Deixe X 1, X 2, ..., X n ser as estatísticas solicitadas com base na amostra aleatória de tamanho n a partir de alguma distribuição contínua.
Permita que a função de distribuição seja F(χ;θ) para Ω em algum espaço de parâmetro com dimensão maior ou igual a 1.
Permita que L < U seja duas estatísticas com base na amostra de tal modo que, para todos os valores indicados, α e P, com 0 < α < 1 e 0 < P < 1, o seguinte se mantém para todos os θ em Ω:
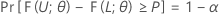
Assim, o intervalo [ L, U] é um intervalo de tolerância de bilateral com um conteúdo = P x 100% e nível de confiança = 100(1 – α)%. Tal intervalo pode ser chamado de intervalo de tolerância bilateral (1 – α, P). Por exemplo, se α = 0,10 e P = 0,85, o intervalo resultante é chamado de intervalo de tolerância bilateral (90% , 0,85).
Se L = –∞ e U < +∞, o intervalo (-∞, U] é chamado de limite de tolerância superior unilateral (1 – α, P). Se L > -∞ e U = +∞, o intervalo [L, +∞) é chamado de limite de tolerância inferior unilateral (1 – α, P).
- Um limite de tolerância inferior unilateral (1 – α, P) também é um limite de tolerância superior unilateral (α, 1 – P).
- Um limite de tolerância inferior unilateral (1 – α )100% do (1 – P)o percentil da distribuição dos dados também é um limite de tolerância inferior unilateral (1 – α, P). Da mesma forma, um limite de confiança superior unilateral (1 – α )100% do Po percentil da distribuição dos dados também é um limite de tolerância superior unilateral (1 – α , P).
- Se L e U forem limites de tolerância inferiores e superiores unilaterais (1 – α/2 , (1 + P )/2), [ L, U ] será um intervalo de tolerância bilateral (1 – α, P ) aproximado. Este método pode ser usado nos casos em que os intervalos de tolerância bilaterais não podem ser obtidos diretamente. Os intervalos de tolerância bilateral resultantes são geralmente conservadores. Consulte Guenther1 e Hahn e Meeker2.
- Guenther, W. C. (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. and Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
Intervalos de tolerância exatos para distribuições normais

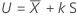
Fator de tolerância para intervalos unilaterais
O fator de tolerância exato para um intervalo unilateral é dado pela seguinte equação: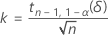
em que tn-1,1-α(δ) é o percentil 1 – α de uma distribuição-t não central com n – 1 graus de liberdade e parâmetro de não centralidade, δ, que é dado pela seguinte fórmula:

Fator de tolerância para intervalos bilaterais
O fator de tolerância exato para um intervalo bilateral é obtido por meio da resolução da seguinte equação para k. Consulte Krishnamoorthy e Mathew1.
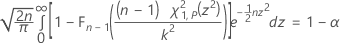
em que Fn – 1 é a função de distribuição acumulada para uma distribuição de qui-quadrado com n – 1 graus de liberdade, e χ21,p é o Po percentil da distribuição qui-quadrado não central com 1 grau de liberdade e parâmetro de não centralidade z2. O lado esquerdo da equação pode ser reescrito como:
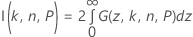
onde:
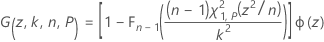
em que Φ(z) é a função densidade de probabilidade da distribuição normal padrão. O Minitab usa uma quadratura Gauss-Legendre de 36 pontos para avaliar I(k, n, P).
Notação
| Termo | Descrição |
|---|---|
| 1 - α | o nível de confiança do intervalo de tolerância |
| P | a cobertura do intervalo de tolerância (a percentagem mínima alvo da população no intervalo) |
| L | o limite inferior do intervalo de tolerância |
| U | o limite superior do intervalo de tolerância |
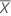 | a média da amostra |
| k | o fator de tolerância (também chamado de fator k) |
| S | o desvio padrão da amostra |
| n | o número de observações na amostra |
| ZP | o Po percentil da distribuição normal padrão |
- Krishnamoorthy, K. e Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
Intervalos de tolerância não paramétricos exatos para distribuições contínuas
O Minitab calcula intervalos de tolerância não paramétricos exatos (1 – α, P), onde 1 – α é o nível de confiança e P é a cobertura (a porcentagem mínima da população-alvo no intervalo). O método não-paramétrico para intervalos de distribuição é um método livre de distribuição. Ou seja, o intervalo de tolerância não-paramétrico não depende da população pai de sua amostra. O Minitab usa um método exato para ambos os intervalos, unilateral e bilateral.
Permita que X 1, X 2 , ... , X n sejam as estatísticas ordenadas com base em uma amostra aleatória de alguma população distribuída continuamente F(x;θ). Logo, com base nas descobertas de Wilks1, 2 e Robbins3, pode-se mostrar que:

onde B indica a função de distribuição acumulada da distribuição beta com parâmetros a = r e b = n – s + 1. Portanto, ( Xr , Xs ) é um intervalo de tolerância sem distribuição porque a cobertura do intervalo tem uma distribuição beta com valores de parâmetro conhecidos, que são independentes da distribuição da população original, F(x;θ).
Intervalos unilaterais
Permita que k seja o maior inteiro que satisfaz o seguinte:

onde Y é uma variável aleatória binomial com n e 1 – P parâmetros. É possível ser mostrado (consulte Krishnamoorthy e Mathew4) que um limite de tolerância inferior unilateral (1 – α, P) é dado por Xk . Da mesma forma, um limite de tolerância superior unilateral (1 – α, P) é dado por X n - k +1. Em ambos os casos, a cobertura real ou efetiva é dada pelo P(Y > k).
Intervalos bilaterais
Permita que k seja o menor inteiro que satisfaz o seguinte:

onde V é uma variável aleatória binomial com n e P parâmetros. Portanto,
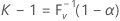
onde F V -1(x) é a função de distribuição acumulativa inversa do V. É possível ser mostrado (consulte Krishnamoorthy e Mathew4) que um intervalo de tolerância bilateral (1 – α, P) pode ser dado como ( Xr , Xs ). O Minitab seleciona s = n - r + 1 de forma que r = ( n – k + 1) / 2. Tanto r como s são arredondados para baixo, para o inteiro mais próximo. A cobertura real ou efetiva é dada por P(V < k – 1).
Notação
| Termo | Descrição |
|---|---|
| 1 – α | o nível de confiança do intervalo de tolerância |
| P | a cobertura do intervalo de tolerância (a porcentagem mínima alvo da população no intervalo) |
| n | o número de observações na amostra |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. e Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
