Neste tópico
Nível de confiança
Como as amostras de dados são aleatórias, é pouco provável que duas amostras de uma mesma população venham a produzir intervalos de tolerância idênticos. Porém, se você coletar muitas amostras, uma certa porcentagem dos intervalos de tolerância resultante conterá a proporção mínima da população que você especificar.
O nível de confiança é a verossimilhança de que o intervalo de tolerância inclui, na verdade, o percentual mínimo. Por exemplo, um engenheiro quer saber o intervalo dentro do qual 99% do produto futuro vai cair, com 98% de confiança. 98% é o nível de confiança para o intervalo de tolerância.
Método
| Nível de confiança | 98% |
|---|---|
| Percentual da população no intervalo | 99% |
Observação
Você pode especificar o nível de confiança para a análise na caixa de diálogo Opções. O Minitab exibe o nível de confiança de destino na tabela Métodos. Por padrão, o nível de confiança é 95%. Para o método não paramétrico, o Minitab calcula o nível de confiança alcançado. O nível de confiança alcançado é o nível de confiança exato que o Minitab calcula. O nível de confiança alcançado é geralmente maior ou igual ao nível de confiança alvo, a menos que o tamanho amostral seja pequeno demais.
Porcentagem da população no intervalo
A porcentagem da população no intervalo é a porcentagem mínima da população que você deseja que o intervalo de tolerância inclua. Por exemplo, um engenheiro quer saber a amplitude que irá incluir 99% do produto futuro, com 98% de confiança. 99% é a porcentagem da população no intervalo de tolerância.
Método
| Nível de confiança | 98% |
|---|---|
| Percentual da população no intervalo | 99% |
N
O tamanho amostral (N) é o número total de observações na amostra. Nestes dados, o tamano amostral é 400.
Estatísticas
| Variável | N | Média | DesvPad |
|---|---|---|---|
| C1 | 400 | 0,604 | 3,671 |
Média
A média resume os valores a amostra com um único valor que representa o centro dos dados. A média é a média dos dados, que é a soma de todas as observações divididas pelo número de observações.
Neste dados, a média é 0,604.
Estatísticas
| Variável | N | Média | DesvPad |
|---|---|---|---|
| C1 | 400 | 0,604 | 3,671 |
StDev
O desvio padrão é a medida mais comum de dispersão, ou quão dispersos os dados estão da média.
Um desvio padrão maior indica que os seus dados estão dispersos mais de maneira mais ampla em torno da média e resultará em um intervalo de tolerância mais amplo. Um desvio padrão menor indica que os dados são distribuídos de forma mais próxima em torno da média e resultará em um intervalo de tolerância estreito.
Nesses dados, o desvio padrão é 3,671.
Estatísticas
| Variável | N | Média | DesvPad |
|---|---|---|---|
| C1 | 400 | 0,604 | 3,671 |
Método normal
Intervalos de tolerância são um intervalo de valores para uma característica de qualidade específica de um produto que provavelmente abrange uma determinada porcentagem da produção futura do produto. Use o intervalo de tolerância do método normal se for possível assumir com segurança que a sua amostra é proveniente de uma população normalmente distribuída.
Se seus dados seguem uma distribuição normal, o método normal será mais preciso e econômico do que o método não paramétrico. O método normal permite alcançar margens menores de erro com menos observações.
O método normal não é robusto para grandes desvios da normalidade. Se você não tiver certeza da distribuição de origem, ou se souber que a distribuição pai não é normal, use o método não-paramétrico.
Interpretação
- Bilateral
- Usar um intervalo bilateral para determinar o intervalo que contém uma certa porcentagem das medições da população.
- Limite superior
- Use um limite superior para determinar o intervalo que indica que uma certa porcentagem das medições da população não será maior do que um limite superior.
- Limite inferior
- Use um limite inferior para determinar o intervalo que indica que uma certa porcentagem das medições população não será menor do que um limite inferior.
Método não paramétrico
Intervalos de tolerância são um intervalo de valores para uma característica de qualidade específica de um produto que provavelmente abrange uma determinada proporção da produção futura do produto. Se não for possível assumir com segurança que a sua amostra é proveniente de uma população normalmente distribuída, você deve usar o intervalo de tolerância do método não paramétrico.
O método não paramétrico requer apenas que os dados sejam contínuos. No entanto, o método não paramétrico necessita de tamanhos amostrais grandes para que os resultados sejam precisos. Se seu tamanho amostral não for grande o bastante, o intervalo não-paramétrico será um intervalo não-informativo que varia de infinito negativo para infinito. Neste caso, o Minitab exibe um intervalo finito com base na amplitude de seus dados. Como resultado, o nível de confiança alcançado é muito menor do que o nível de confiança alvo.
Interpretação
- Bilateral
- Usar um intervalo bilateral para determinar o intervalo que contém uma certa porcentagem das medições da população.
- Limite superior
- Use um limite superior para determinar o intervalo que indica que uma certa porcentagem das medições da população não será maior do que um limite superior.
- Limite inferior
- Use um limite inferior para determinar o intervalo que indica que uma certa porcentagem das medições população não será menor do que um limite inferior.
Confiança alcançada
Para o método não paramétrico, o Minitab calcula o nível de confiança alcançado. Este é o nível de confiança exato obtido a partir de sua amostra. Em geral, será maior ou igual ao nível de confiança alvo, a menos que o tamanho de amostra seja muito pequeno.
Interpretação
- Bilateral
- Usar um intervalo bilateral para determinar o intervalo que contém uma certa porcentagem das medições da população.
- Limite superior
- Use um limite superior para determinar o intervalo que indica que uma certa porcentagem das medições da população não será maior do que um limite superior.
- Limite inferior
- Use um limite inferior para determinar o intervalo que indica que uma certa porcentagem das medições população não será menor do que um limite inferior.
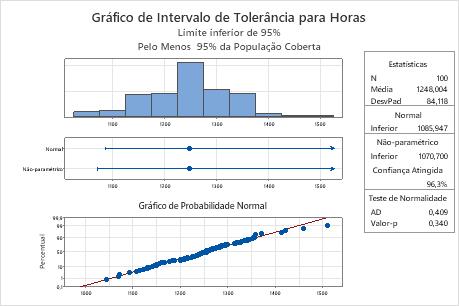
Gráfico de intervalo de tolerância
- Histograma: mostra a distribuição de seus dados amostrais. Cada barra no histograma representa a frequência de dados dentro de um intervalo.
- Gráficos de intervalo: mostram a média e limites superior e/ou inferior do intervalo de tolerância para cada método. Uma linha vertical na extremidade do intervalo representa um limite, e uma seta indica que não existe nenhum limite para aquele lado do intervalo.
- Gráfico de probabilidade normal: mostra o quão bem seus dados ajustam a distribuição normal. Se seus dados forem normalmente distribuídos, os pontos de dados no gráfico de probabilidade formam uma linha reta.
- Tabela de estatística: exibe o tamanho amostral, média e desvio padrão.
- Tabela normal: exibe os limites superior e/ou inferior do intervalo de tolerância do método normal.
- Tabela não-paramétrica: exibe os limites superior e/ou inferior do intervalo de tolerância do método não paramétrico e o nível de confiança alcançado.
- Tabela do teste de Normalidade: mostra o valor de p e o valor do teste de normalidade Anderson-Darling. Para determinar se você pode assumir que os dados seguem uma distribuição normal, compare o valor de p do teste de normalidade com o nível de significância (α). Se o valor de p for menor ou igual ao nível de significância, é possível concluir que seus dados não seguem uma distribuição normal. Neste caso, você deve usar o intervalo de tolerância do método não paramétrico.
Interpretação
O gráfico de probabilidade normal mostra que os pontos representados graficamente formam uma linha reta aproximada, o que indica que os dados seguem uma distribuição normal. Além disso, o valor de p para o teste de normalidade é 0.340, a qual é maior do que o nível de significância (α = 0,05). Portanto, não há evidências suficientes para concluir que os dados não seguem uma distribuição normal. O engenheiro pode usar os resultados normais do método.
O limite inferior normal é 1085.947, de forma que o engenheiro tem 95% de confiança de que pelo menos 95% de todas as lâmpadas excedem aproximadamente 1086 horas de tempo de queima. Para todas as lâmpadas, a média de tempo de queima é de aproximadamente 1248 horas e o desvio padrão é de aproximadamente 84,1.