Um engenheiro de qualidade quer avaliar a duração de lâmpadas fabricadas pela empresa. O engenheiro coleta uma amostra aleatória de 100 lâmpadas e registra os tempos de queima até a falha. O engenheiro quer calcular o limite de tolerância inferior (que é o tempo de queima que pelo menos 95% todas as lâmpadas ultrapassam).
- Abra os dados amostrais, TempoVidaLâmpada.MWX.
- Selecione .
- Na lista suspensa, selecione Uma ou mais amostras, cada uma em uma coluna, em seguida, insira Horas.
- Clique em Opções.
- Em Intervalo de tolerância, selecione Limite inferior.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
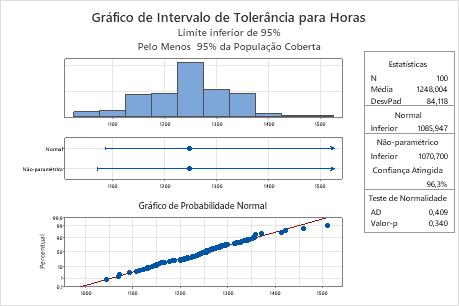
O gráfico de probabilidade normal mostra que os pontos representados graficamente formam uma linha reta aproximada, o que indica que os dados seguem uma distribuição normal. Além disso, o valor de p para o teste de normalidade é 0,340, a qual é maior do que o nível de significância (α = 0,05). Portanto, não há evidências suficientes para concluir que os dados não seguem uma distribuição normal. O engenheiro pode usar os resultados normais do método.
O limite inferior normal é 1085,947, de forma que o engenheiro tem 95% de confiança de que pelo menos 95% de todas as lâmpadas excedem aproximadamente 1086 horas de tempo de queima. Para todas as lâmpadas, a média de tempo de queima é de aproximadamente 1248 horas e o desvio padrão é de aproximadamente 84,1.
Método
| Nível de confiança | 95% |
|---|---|
| Percentual da população no intervalo | 95% |
Estatísticas
| Variável | N | Média | DesvPad |
|---|---|---|---|
| Horas | 100 | 1248,004 | 84,118 |
Limite de 95% Tolerância Inferior
| Variável | Método Normal | Método Não-paramétrico | Confiança Atingida |
|---|---|---|---|
| Horas | 1085,947 | 1070,700 | 96,3% |