Estimativas de máxima verossimilhança
As estimativas de máxima verossimilhança dos parâmetros na distribuição são calculadas através da maximização da função de verossimilhança relacionada aos parâmetros. Para um dado ajuste de dados, as estimativas de máxima verossimilhança são os valores mais prováveis dos parâmetros de distribuição.
O algorítmo de Newton-Raphson é usado para calcular as estimativas de verosimilhança máximas dos parâmetros de distribuição. O algoritmo de Newton-Raphson é um método numérico iterativo para calcular o máximo de uma função. 1
Observação
O Minitab calcula as estimativas do parâmetro usando o método de máxima verossimilhança para todas as distribuições exceto a distribuição lognormal. Para a distribuição lognormal, o Minitab calcula as estimativas não viciadas de parâmetro.
Distribuições de probabilidades
Distribuição lognormal
| FDP |
 |
| FDA |
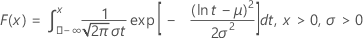 |
| Média |
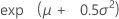 |
| Stdev |
 |
| Termo | Descrição |
|---|---|
| μ | Parâmetro de escala |
| σ | Parâmetro de forma |
Distribuição gama
| FDP |
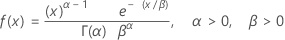 |
| FDA |
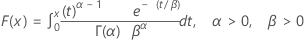 |
| Média | αβ |
| Stdev | αβ2 |
| Termo | Descrição |
|---|---|
| α | Parâmetro de forma |
| β | Parâmetro de escala |
Distribuição exponencial
| FDP |
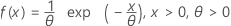 |
| FDA |
 |
| Média | θ |
| Stdev | θ |
| Termo | Descrição |
|---|---|
| θ | Parâmetro de escala |
Distribuição do menor valor extremo
| FDP |
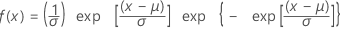 |
| FDA |
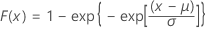 |
| Média |
 |
| Stdev |
 |
| Termo | Descrição |
|---|---|
| μ | Parâmetro de localização |
| σ | Parâmetro de escala |
| Y | Constante de Euler (aproximadamente igual a 0,5772) |
Distribuição Weibull
| FDP |
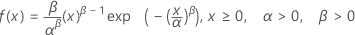 |
| FDA |
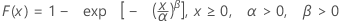 |
| Média |
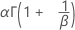 |
| Stdev |
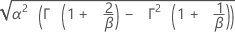 |
| Termo | Descrição |
|---|---|
| α | Parâmetro de escala |
| β | Parâmetro de forma |
Distribuição do maior valor extremo
| FDP |
 |
| FDA |
 |
| Média |
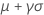 |
| Stdev |
 |
| Termo | Descrição |
|---|---|
| μ | Parâmetro de localização |
| σ | Parâmetro de escala |
| Y | Constante de Euler (aproximadamente igual a 0,5772) |
Distribuição logística
| FDP |
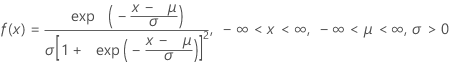 |
| FDA |
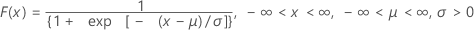 |
| Média | μ |
| Stdev |
 |
| Termo | Descrição |
|---|---|
| μ | Parâmetro de localização |
| σ | Parâmetro de escala |
Distribuição loglogística
| FDP |
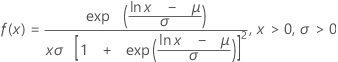 |
| FDA |
 |
| Média |
 |
| Stdev |
 |
| Termo | Descrição |
|---|---|
| μ | Parâmetro de localização |
| σ | Parâmetro de escala |
