Principais resultados para Intervalos de tolerância (distribuição não normal)

Conclua os passos a seguir para interpretar intervalos de tolerância.

Neste tópico

Etapa 1: Avaliar o ajuste de distribuição dos dados
Etapa 2: Examinar o intervalo de tolerância do método adequado

Etapa 1: Avaliar o ajuste de distribuição dos dados

O Minitab fornece intervalos de tolerância para um método que usa uma distribuição e um método não paramétrico. Se você puder assumir com segurança que seus dados seguem a distribuição, será possível usar o intervalo de tolerância para o método que usa a distribuição. Se você não pode seguramente assumir que seus dados seguem a distribuição, então você deve tentar uma distribuição diferente ou o intervalo de tolerância para o método não-paramétrico.

Para determinar se você pode assumir que os dados seguem a distribuição, compare o valor-p a partir do teste de Anderson-Darling ao nível de significância (α). Um nível de significância de 0,05 indica um risco de 5% de concluir que os dados não seguem a distribuição quando eles realmente a seguem.

Valor-p ≤ α: os dados não seguem a distribuição (você deve rejeitar H₀): Se o valor de p for menor ou igual ao nível significativo, é possível concluir que seus dados não seguem a distribuição. Neste caso, você deve tentar uma distribuição diferente ou o intervalo de tolerância para o método não-paramétrico.
Valor-p > α: Você não tem evidências suficientes para concluir que os dados não seguem a distribuição (Falha ao rejeitar H₀): Se o valor de p for maior do que o nível significativo, não há evidências suficientes para concluir que os dados não seguem uma distribuição normal. Neste caso, é possível usar o intervalo de tolerância para o método que usa a distribuição.

Principais resultados: Gráfico de probabilidade e valor de p

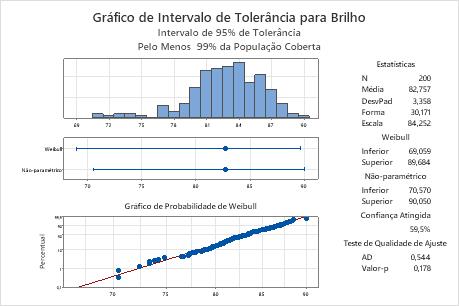
O gráfico de probabilidade mostra que os pontos representados graficamente caem ao longo da linha ajustada da distribuição de Weibull, o que indica que os dados seguem uma distribuição Weibull. Além disso, o valor-p do teste de qualidade de ajuste é de 0,178, que é maior do que o nível de significância de 0,05. Como não é possível concluir que os dados não seguem a distribuição Weibull, você pode usar o intervalo para a distribuição Weibull.

Etapa 2: Examinar o intervalo de tolerância do método adequado

O Minitab fornece intervalos de tolerância para o método que usa a distribuição e o método não-paramétrico que não supõe uma distribuição específica. É possível criar um intervalo de tolerância bilateral, ou um intervalo de tolerância unilateral que fornece um limite superior ou um limite inferior.

Bilateral

Use um intervalo bilateral para determinar um intervalo que contém uma certa porcentagem mínima das medidas da população.

Estatísticas

Variável	N	Média	DesvPad
Brilho	200	82,757	3,358

Intervalo de 95% de Tolerância

Variável	Método Weibull	Método Não-paramétrico	Confiança Atingida
Brilho	(69,059; 89,684)	(70,570; 90,050)	59,54%

Principais resultados: 95% de intervalo de tolerância

O intervalo Weibull varia de aproximadamente 69,1 a 89,7, logo, o fabricante pode ter 95% de confiança de que pelo menos 99% de todos os lotes de polpa cairão nesse intervalo. Para todos os lotes da polpa, o nível médio de brilho é de aproximadamente 82,8.

Limite superior

Use um limite superior para determinar um limite que exceda uma certa porcentagem mínima das medidas da população.

Limite de 95% de Tolerância Superior

Variável	Método Weibull	Método Não-paramétrico	Confiança Atingida
Brilho	89,131	90,050	86,60%

Principais resultados: limite de tolerância superior de 95%

Neste exemplo, o limite superior Weibull é de 89,131, logo, você pode ter 95% de confiança que 99% de todos os lotes da polpa terão medidas de brilho de 89,131 ou menos. Caso não possa assumir que os dados seguem uma distribuição Weibull, encontre uma distribuição diferente que se ajuste ou considere o limite superior não paramétrico de 90,50. Para o método não paramétrico, a confiança alcançada é de 86,60% que é muito menor do que o valor alvo de 95%. Este resultado indica que seu tamanho de amostra é muito pequeno para o método não paramétrico ser preciso.

Limite inferior

Use um limite inferior para determinar um limite que é menor do que uma certa porcentagem mínima das medidas de população.

Limite de 95% Tolerância Inferior

Variável	Método Weibull	Método Não-paramétrico	Confiança Atingida
Brilho	71,105	70,570	86,60%

Principais resultados: limite de tolerância inferior de 95%

Neste exemplo, o limite inferior Weibull é de 71,105, logo, é possível ter 95% de confiança de que 99% de todos os lotes da polpa terão medidas de brilho de 71,105 ou mais. Caso não possa supor que os dados seguem uma distribuição Weibull, encontre uma distribuição diferente que se ajuste ou considere o limite inferior não-paramétrico de 70,570. Para o método não-paramétrico, a confiança alcançada é de 86,60% que é muito menor do que o valor alvo de 95%. Este resultado indica que seu tamanho amostral é muito menor para o método não-paramétrico para ser exato.