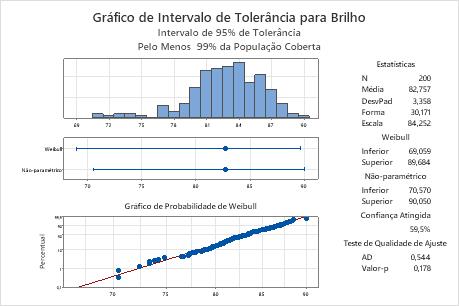
Um fabricante deseja avaliar a variabilidade de seu processo de branqueamento de papel. O fabricante coleta aleatoriamente 200 amostras de polpa e registra o nível de brilho. O fabricante deseja calcular um intervalo dentro do qual o brilho de pelo menos 99% dos lotes de polpa deve cair.
- Abra os dados amostrais, BrilhodePolpa.MWX.
- Selecione .
- Em Variáveis insira Brilho.
- Na Porcentagem mínima do intervalo da população, insira 99.
- Clique em OK.
Interpretar os resultados
O gráfico de probabilidade mostra que os pontos representados graficamente caem ao longo da linha ajustada da distribuição de Weibull, o que indica que os dados seguem uma distribuição Weibull. Além disso, o valor-p do teste de qualidade de ajuste é de 0,178, que é maior do que o nível de significância de 0,05. Como não é possível concluir que os dados não seguem a distribuição Weibull, você pode usar o intervalo para a distribuição Weibull.
O intervalo Weibull varia de aproximadamente 69,1 a 89,7, logo, o fabricante pode ter 95% de confiança de que pelo menos 99% de todos os lotes de polpa cairão nesse intervalo. Para todos os lotes da polpa, o nível médio de brilho é de aproximadamente 82,8.
Método
| Distribuição | Weibull |
|---|---|
| Nível de confiança | 95% |
| Percentual da população no intervalo | 99% |
Estatísticas
| Variável | N | Média | DesvPad |
|---|---|---|---|
| Brilho | 200 | 82,757 | 3,358 |
Parâmetros da distribuição
| Variável | Forma | Escala |
|---|---|---|
| Brilho | 30,171 | 84,252 |
Intervalo de 95% de Tolerância
| Variável | Método Weibull | Método Não-paramétrico | Confiança Atingida |
|---|---|---|---|
| Brilho | (69,059; 89,684) | (70,570; 90,050) | 59,54% |