Neste tópico
Etapa 1: Visualize o ajuste da distribuição normal
Use os gráficos de probabilidade normal para avaliar se os dados originais e transformados seguem a distribuição normal de perto.
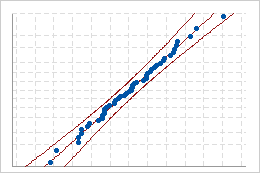
Bom ajuste
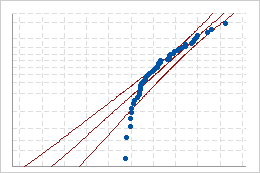
Ajuste ruim
Observação
Se os dados originais forem normalmente distribuídos, o Minitab exibe apenas um único gráfico de probabilidade e não executa a transformação de Johnson.
Etapa 2: Avalie o ajuste da distribuição normal
Use o valor de p para avaliar se você pode assumir que os dados originais e dados transformados seguem a distribuição normal.
- Um valor de p menor do que alfa indica que a distribuição normal não é um bom ajuste.
- Um valor de p maior ou igual a alfa indica que não há evidências suficientes de um mal ajuste de distribuição. É possível assumir que os dados seguem a distribuição normal.
Se a transformação Johnson for eficaz, o valor de p para os dados transformados é maior do que alfa.
Importante
Tenha cuidado ao interpretar os resultados a partir de uma amostra muito pequena ou muito grande. Se você tem uma amostra muito pequena, um teste de qualidade de ajuste pode não ter poder suficiente para detectar desvios significativos da distribuição. Se você tem uma amostra muito grande, o teste pode ser tão poderosa a ponto de detectar até mesmo pequenos desvios da distribuição que não têm nenhuma significância prática. Além dos gráficos de probabilidade, utilize os valores de p para avaliar o ajuste de distribuição.
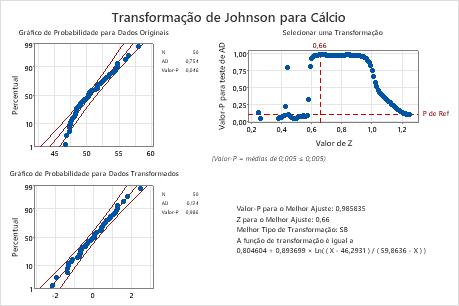
Resultados principais: valor de p
Nestes resultados, o valor de p (0,046) para os dados originais é menor do que alfa (0,10), o que indica que os dados originais de cálcio não são normais. Para os dados transformados, o valor de p (0,986) é maior do que alfa. Portanto, é possível assumir que os dados transformados seguem uma distribuição normal.
Etapa 3: Examine a função de transformação
O Minitab mostra os parâmetros da função de transformação de Johnson que produz o melhor ajuste. O Minitab usa essa função para transformar os dados originais.
Por exemplo, suponha que a função de transformação de Johnson é 0,762475 + 0,870902 × Ln((X – 46,3174 ) / (59,6770 – X)). Se o valor de dados original para X for 50, então o valor de dados transformados de 50 é calculado como 0,762475 + 0,870902 × Ln((50 – 46,3174) / (59,677 – 50)), que é igual –0,07893.
Observação
Para armazenar todos os valores de dados transformados na worksheet, insira uma coluna de armazenamento quando executar a análise.
Para obter mais informações sobre o algoritmo que o Minitab usa para definir a função de transformação de Johnson, acesse Métodos e fórmulas para transformações em Identificação de distribuição individual e clique em "Métodos e fórmulas para a transformação de Johnson".
