Neste tópico
Gráfico de probabilidade de dados originais e transformados
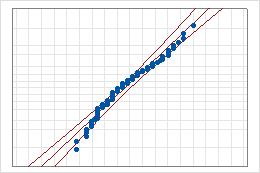
- Linha central
- O percentil esperado a partir da distribuição com base em estimativas de parâmetros de máxima verossimilhança.
- Linhas do limite de confiança
- A linha curva à esquerda indica os limites inferiores dos intervalos de confiança para os percentis. A linha curva direita indica os limites superiores dos intervalos de confiança para os percentis.
Interpretação
Use os gráficos de probabilidade normal para avaliar se os dados originais e transformados seguem a distribuição normal de perto.
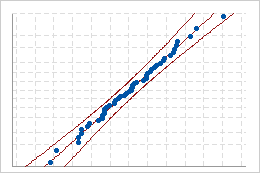
Bom ajuste
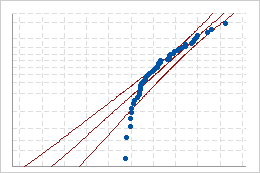
Ajuste ruim
Observação
Se os dados originais forem normalmente distribuídos, o Minitab exibe apenas um único gráfico de probabilidade e não executa a transformação de Johnson.
N
O número de valores não faltantes na amostra. N é a contagem de todos os valores observados.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interpretação
Use N para avaliar o tamanho da amostra.
Importante
Tenha cuidado ao interpretar os resultados a partir de uma amostra muito pequena ou muito grande. Se você tem uma amostra muito pequena, um teste de qualidade de ajuste pode não ter poder suficiente para detectar desvios significativos da distribuição. Se você tem uma amostra muito grande, o teste pode ser tão poderosa a ponto de detectar até mesmo pequenos desvios da distribuição que não têm nenhuma significância prática. Além dos gráficos de probabilidade, utilize os valores de p para avaliar o ajuste de distribuição.
AD
A estatística do teste de qualidade de ajuste de Anderson-Darling (AD) é uma medida dos desvios entre a linha ajustada (com base na distribuição selecionada) e a função da etapa não paramétrica (com base nos pontos de dados). A estatística Anderson-Darling é uma distância ao quadrado que é ponderada mais pesadamente nas caudas da distribuição.
Interpretação
O Minitab usa a estatística de Anderson-Darling para calcular o valor de p. O valor de p é uma probabilidade que mede a evidência contra a hipótese nula de que os dados seguem a distribuição.
Geralmente, os valores substancialmente menores para a estatística de Anderson-Darling indicam que os dados seguem uma distribuição mais de próxima. No entanto, evite comparar diretamente os valores de AD em diferentes distribuições quando os valores de AD estão próximos, porque as estatísticas AD são distribuídos de forma diferente para diferentes distribuições. Para comparar melhor o ajuste de diferentes distribuições, use critérios adicionais, como gráficos de probabilidade, valores de p e seu conhecimento do processo.
Valor de p
Para os valores de dados originais e transformados, o Minitab informa um valor de p para o teste de normalidade Anderson-Darling (AD). O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. Para um teste de normalidade, a hipótese nula é que os dados seguem a distribuição normal. Portanto, os valores de p menores fornecem evidência mais forte de que os dados não seguem a distribuição normal.
Interpretação
Use o valor de p para avaliar se os dados originais e transformados seguem a distribuição normal. Um valor de p maior geralmente indica um melhor ajuste para os dados.
- Um valor de p menor do que alfa indica que a distribuição normal não é um bom ajuste.
- Um valor de p maior ou igual a alfa indica que não há evidências suficientes de um mal ajuste de distribuição. É possível assumir que os dados seguem a distribuição normal.
Se a transformação Johnson for eficaz, o valor de p para os dados transformados é maior do que alfa.
Importante
Tenha cuidado ao interpretar os resultados a partir de uma amostra muito pequena ou muito grande. Se você tem uma amostra muito pequena, um teste de qualidade de ajuste pode não ter poder suficiente para detectar desvios significativos da distribuição. Se você tem uma amostra muito grande, o teste pode ser tão poderosa a ponto de detectar até mesmo pequenos desvios da distribuição que não têm nenhuma significância prática. Além dos gráficos de probabilidade, utilize os valores de p para avaliar o ajuste de distribuição.
Gráfico Selecionar uma Transformação
O gráfico Selecionar uma Transformação representa graficamente o valor de p calculado do teste de normalidade de AD para cada valor de Z para diferentes funções de transformação de Johnson. Para encontrar o Z ideal, a transformação de Johnson utiliza uma grade de Zs ao longo de um intervalo entre 0,25 e 1,25, com um incremento de 0,01 para uma grande variedade de distribuições. O Minitab calcula o valor de p para os dados transformados e cada Z seleciona uma função de transformação que tem o maior valor de p que é superior ao critério de p-valor especificado para a análise.
Interpretação
Use o gráfico Selecionar uma Transformação para visualizar como a função de transformação de Johnson é selecionada para produzir o melhor ajuste para os dados. A linha de referência horizontal mostra o critério do valor de p especificado para a análise. A linha de referência vertical mostra o valor de Z para a transformação que produz o melhor ajuste. Este valor máximo de Z corresponde ao valor de p mínimo para o teste de normalidade de AD.
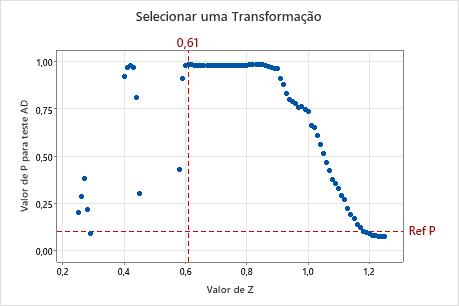
Observação
A tabela abaixo do gráfico (não mostrado aqui) mostra as estimativas dos parâmetros para a melhor função de transformação. Para obter mais informações sobre o algoritmo que o Minitab usa para a função de transformação de Johnson, acesse Métodos e fórmulas para transformações em Identificação de distribuição individual e clique em "Métodos e fórmulas para a transformação de Johnson".
Valor de P para o melhor ajuste
O valor de p para o melhor ajuste indica o valor de p para a função de transformação de Johnson que resulta no melhor ajuste dos dados transformados para a distribuição normal. Esse valor de p, arredondado para o milhar mais próximo, também é mostrado no gráfico de probabilidade para os dados transformados.
Para obter informações sobre como interpretar o valor de p, consulte a seção sobre o valor de p.
Para obter informações sobre como o Minitab seleciona a função de transformação Johnson com o melhor ajuste, consulte a seção sobre Selecionar um gráfico transformação.
Z para o melhor ajuste
O valor de Z para o melhor ajuste indica o valor de Z para a função de transformação de Johnson que resulta no melhor ajuste dos dados transformados para a distribuição normal. O valor de Z ideal corresponde ao valor de p para melhor ajuste, conforme mostrado no gráfico da melhor transformação.
Para obter informações sobre como o Minitab usa o valor de Z para selecionar a função de transformação Johnson com o melhor ajuste, consulte a seção sobre Selecionar um gráfico transformação.
Melhor tipo de transformação
A transformação de Johnson faz uma seleção ótima de uma das três famílias de distribuição: S B, S L e S U, onde B, L e U referem-se às variáveis como limitada, lognormal e ilimitada, respectivamente. O Minitab usa a função de distribuição selecionada para transformar os dados a seguir uma distribuição normal.
Para obter mais informações sobre o algoritmo que o Minitab usa para definir a função de transformação de Johnson, acesse Métodos e fórmulas para transformações em Identificação de distribuição individual e clique em "Métodos e fórmulas para a transformação de Johnson".
Função da transformação de Johnson
O Minitab mostra os parâmetros da função de transformação de Johnson que produz o melhor ajuste. O Minitab usa essa função para transformar os dados originais.
Por exemplo, suponha que a função de transformação de Johnson é 0,762475 + 0,870902 × Ln((X – 46,3174) / (59,6770 – X)). Se o valor de dados original para X for 50, então o valor de dados transformados de 50 é calculado como 0,762475 + 0,870902 × Ln((50 – 46,3174) / (59,6770 – 50)), que é igual –0,07893.
Observação
Para armazenar todos os valores transformados na worksheet, insira uma coluna de armazenamento quando executar a análise.
Para obter mais informações sobre o algoritmo que o Minitab usa para definir a função de transformação de Johnson, acesse Métodos e fórmulas para transformações em Identificação de distribuição individual e clique em "Métodos e fórmulas para a transformação de Johnson".
