Transformação Box-Cox
A transformação de Box-Cox calcula um valor de lambda, como mostrado na tabela a seguir, o que minimiza o desvio padrão de uma variável de transformada padronizada. A transformação resultante é Yλ quando λ ҂ 0 e In Y quando λ = 0.
O método Box-Cox pesquisa através de muitos tipos de transformações. A tabela a seguir mostra algumas transformações comuns onde Y' é a transformação do Y dos dados.
| Valor lambda (λ) | Transformação |
|---|---|
 |
 |
 |
 |
 |
 |
 |
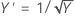 |
 |
 |
Algoritmo para a transformação de Johnson
A transformação Johnson seleciona de maneira ideal uma das três famílias de distribuição para transformar os dados para seguir uma distribuição normal.
| Família Johnson | Função da transformação | Intervalo |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η, λ > 0, –∞ < γ < ∞ , –∞ < ε < ∞, ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0, –∞ < γ < ∞, –∞ < ε < ∞, ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ] , em que
Sinh–1(x) = ln [x + sqrt (1 + x2)] |
η, λ > 0, –∞ < γ < ∞, –∞ < ε < ∞, –∞ < x < ∞ |
O algoritmo usa o seguinte procedimento:
- Considera quase todas as funções de transformação potenciais do sistema de Johnson.
- Estima os parâmetros da função, utilizando o método descrito no Chou, et al.1
- Transforma os dados usando a função de transformação.
- Calcula a estatística de Anderson-Darling e o valor de correspondente aos dados transformados.
- Seleciona a função de transformação que tem o maior valor de p que é superior ao critério de valor de p (o padrão é 0,10) que você especificar na caixa de diálogo Transformar. De outra forma, nenhuma transformação é apropriada.
Notação
| Termo | Descrição |
|---|---|
| SB | A distribuição da família Johnson com a variável delimitada (B) |
| SL | A distribuição da família Johnson com a variável lognormal (B) |
| SU | A distribuição da família Johnson com a variável não delimitada (B) |
Para mais informações sobre a transformação Johnson, consulte Chou, et al.1 O Minitab substitui o teste de normalidade de Shapiro-Wilks utilizado nesse texto com o teste de Anderson-Darling.
Para obter informações sobre o gráfico de probabilidade, percentis e seus intervalos confiança, acesse Métodos e fórmulas para distribuições em Identificação de distribuição individual.
