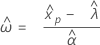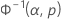Neste tópico
Gráfico de probabilidade
Os gráficos de probabilidade incluem:
- Pontos, que são os percentis estimados para corresponder às probabilidades de um ajuste de dados ordenado.
- Linhas centrais que são o percentil esperado da distribuição com base em estimativas de parâmetros de máxima verossimilhança. Se a distribuição for um bom ajuste para os dados, os pontos terão queda junto com a linha central.
Probabilidades estimadas
O Minitab estima a probabilidade (P) que é utilizada para calcular os pontos do gráfico, usando os métodos a seguir.
- Rank Mediano (método de Benard)
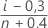
- Rank mediano (estimativa de Herd-Johnson)

- Modificação de Kaplan-Meier (Hazen)
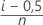
- estimativa de limite de produto de Kaplan-Meier

Notação
| Termo | Descrição |
|---|---|
| n | Número de observações |
| ii | Rank da ia observação ordenada x(i), onde x(1), x(2),...x(n) são as estatísticas de ordem ou os dados ordenados do menor para o maior |
Pontos do gráfico
A linha do meio do gráfico de probabilidade é construída usando os cálculos das coordenadas x e y nesta tabela.
| Distribuição | coordenada x | coordenada y |
|---|---|---|
| Menor valor extremo | x | ln(–ln(1 – p)) |
| Maior valor extremo | x | ln(–ln p) |
| Weibull | ln(x) | ln(–ln(1 – p)) |
| Weibull para 3 parâmetros | ln(x – limite) | ln(–ln(1 – p)) |
| Exponencial | ln(x) | ln(–ln(1 – p)) |
| Exponencial para 2 parâmetros | ln(x – limite) | ln(–ln(1 – p)) |
| Normal | x | Φ–1norm |
| Lognormal | ln(x) | Φ–1norm |
| Lognormal para 3 parâmetros | ln(x – limite) | Φ–1norm |
| Logística | x |
 |
| Loglogística | ln(x) |
 |
| Loglogística para 3 parâmetros | ln(x – limite) |
 |
| Gama | x | Φ–1gama |
| Gama para 3 parâmetros | ln(x – limite) | Φ–1gama |
Observação
Como os pontos do gráfico não dependem de nenhuma distribuição, eles são os mesmos (antes da transformação) para qualquer gráfico de probabilidade. No entanto, a linha ajustada é diferente, dependendo da distribuição paramétrica escolhida.
Notação
| Termo | Descrição |
|---|---|
| p | A probabilidade estimada |
| Φ-1norm | Valor retornado para p pela FDA inversa para a distribuição normal padrão |
| Φ-1gama | Valor retornado para p pela FDA inversa para a distribuição gama incompleta |
| ln(x) | O log natural de x |
Percentis e erros padrão dos percentis
Percentil é um valor em uma escala de 100 que indica a porcentagem de uma distribuição que é inferior ou igual a esse valor. Por padrão, o Minitab exibe tabelas de percentis para análise de distribuição paramétrica para percentis comuns.
Os erros padrão para as estimativas dos percentis são a raiz quadrada das variâncias.
 ,
,  ,
,  ,
,  ,
,  ,
, 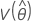 ,
, 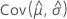 ,
, 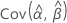 , e
, e 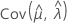 denota as variâncias e covariâncias dos MLEs de μ, σ, α, β, λ e θ retirados do elemento apropriado da inversa da matriz de informação de Fisher.
denota as variâncias e covariâncias dos MLEs de μ, σ, α, β, λ e θ retirados do elemento apropriado da inversa da matriz de informação de Fisher.
As fórmulas utilizadas para as estimativas de percentis e variâncias são as seguintes:
Distribuição do menor valor extremo
- Percentil
-
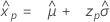
- Variância
-

Distribuição do maior valor extremo
- Percentil
-
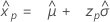
- Variância
-

Distribuição Weibull
- Percentil
-

- Variância
-
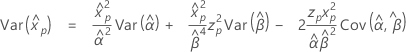
Distribuição Weibull para 3 parâmetros
- Percentil
-
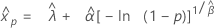
- Variância
-
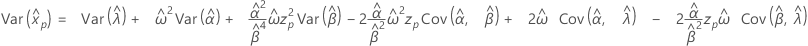
Distribuição exponencial
- Percentil
-

- Variância
-

Distribuição exponencial para 2 parâmetros
- Percentil
-
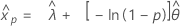
- Variância
-

Distribuição normal
- Percentil
-
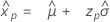
- Variância
-

Distribuição lognormal
- Percentil
-

- Variância
-

Distribuição lognormal para 3 parâmetros
- Percentil
-

- Variância
-

Distribuição logística
- Percentil
-
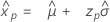
- Variância
-

Distribuição Loglogística
- Percentil
-

- Variância
-

Distribuição Loglogística para 3 parâmetros
- Percentil
-

- Variância
-

Distribuição gama
- Percentil
-
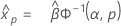
- Variância
-
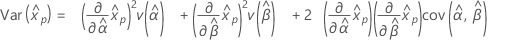
Distribuição gama para 3 parâmetros
- Percentil
-
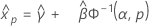
- Variância
-
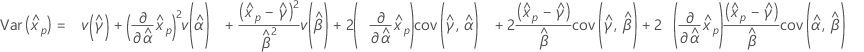
Limite de confiança para percentis
| Distribuição | Limites de confiança |
|---|---|
| Menor valor extremo |
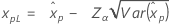 |
| Maior valor extremo |
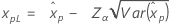 |
| Normal |
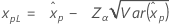 |
| Logística |
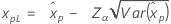 |
| Weibull |
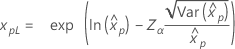 |
| Exponencial |
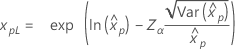 |
| Lognormal |
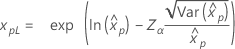 |
| Loglogística |
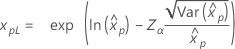 |
| Weibull para 3 parâmetros |
Se λ < 0:
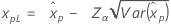 Se λ ≥ 0:
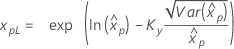 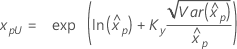 |
| Exponencial para 2 parâmetros |
Se λ < 0:
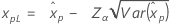 Se λ ≥ 0:
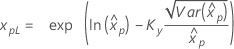 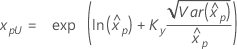 |
| Lognormal para 3 parâmetros |
Se λ < 0:
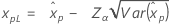 Se λ ≥ 0:
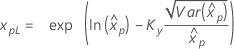 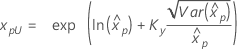 |
| Loglogística para 3 parâmetros |
Se λ < 0:
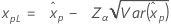 Se λ ≥ 0:
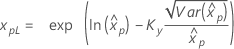 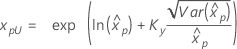 |
Notação
| Termo | Descrição |
|---|---|
| Kγ | O (1 + γ) / 2 percentil de uma distribuição normal padrão |