Etapa 1: Visualize o ajuste da distribuição
Use o gráfico de probabilidade normal para avaliar o quanto seus dados se aproximam de cada distribuição.
Se a distribuição for um bom ajuste para os dados, os pontos devem cair próximos à linha de distribuição ajustada. Pontos distantes da linha reta indicam que o ajuste é inaceitável.
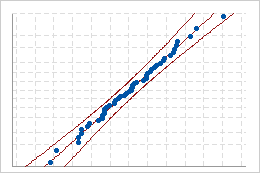
Bom ajuste
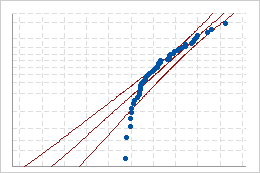
Ajuste ruim
Além dos gráficos de probabilidade, use as medidas de qualidade do ajuste, como os valores de p e o seu conhecimento prático do processo, para avaliar o ajuste de distribuição.
Etapa 2: Avalie o ajuste da distribuição
Use o valor de p para avaliar o ajuste da distribuição.
- P ≤ α: Os dados não seguem a distribuição (Rejeitar H0)
- Se o valor de p for inferior ou igual ao nível de significância, você deve rejeitar a hipótese nula e concluir que os seus dados não seguem a distribuição.
- P > α: Não é possível concluir que os dados não seguem a distribuição (Falha ao rejeitar H0)
- Se o valor de p for maior do que o nível de significância, você deixa de rejeitar a hipótese nula. Não há evidências suficientes para concluir que os dados não seguem a distribuição. É possível assumir que os dados seguem a distribuição.
- Escolha a distribuição que seja mais comumente usada em seu setor ou aplicativo.
- Escolha a distribuição que fornece os resultados mais conservadores. Por exemplo, se você está realizando análise de capacidade, pode realizá-la usando diferentes distribuições e, em seguida, escolher a distribuição que produz a maioria dos índices de capacidade conservadores. Para obter mais informações, acesse Percentis de distribuição para Identificação de distribuição individual e clique em "Porcentagens e percentis".
- Escolha a distribuição mais simples que se ajusta bem os seus dados. Por exemplo, se distribuições de 2 parâmetros e de 3 parâmetros fornecem ambas um bom ajuste, é possível escolher a distribuição de 2 parâmetros mais simples.
Importante
Tenha cuidado ao interpretar os resultados a partir de uma amostra muito pequena ou muito grande. Se você tem uma amostra muito pequena, um teste de qualidade de ajuste pode não ter poder suficiente para detectar desvios significativos da distribuição. Se você tem uma amostra muito grande, o teste pode ser tão poderosa a ponto de detectar até mesmo pequenos desvios da distribuição que não têm nenhuma significância prática. Além dos gráficos de probabilidade, utilize os valores de p para avaliar o ajuste de distribuição.
Teste de Qualidade de Ajuste
| Distribuição | AD | P | TRV P |
|---|---|---|---|
| Normal | 0,754 | 0,046 | |
| Transformação de Box-Cox | 0,414 | 0,324 | |
| Lognormal | 0,650 | 0,085 | |
| Lognormal de 3 Parâmetros | 0,341 | * | 0,017 |
| Exponencial | 20,614 | <0,003 | |
| Exponencial de 2 Parâmetros | 1,684 | 0,014 | 0,000 |
| Weibull | 1,442 | <0,010 | |
| Weibull de 3 Parâmetros | 0,230 | >0,500 | 0,000 |
| Menor Valor Extremo | 1,656 | <0,010 | |
| Maior Valor Extremo | 0,394 | >0,250 | |
| Gama | 0,702 | 0,071 | |
| Gama de 3 Parâmetros | 0,268 | * | 0,006 |
| Logística | 0,726 | 0,034 | |
| Loglogística | 0,659 | 0,050 | |
| Loglogística de 3 Parâmetros | 0,432 | * | 0,027 |
| Transformação de Johnson | 0,124 | 0,986 |
Principais resultados: P
Nestes resultados, várias distribuições têm um valor de p maior do que 0,05. A distribuição Weibull para 3 parâmetros (P > 0,500) e a distribuição de maior valor extremo (P > 0,250) têm os maiores valores de p, e parecem ajustar os dados de amostra melhor do que as outras distribuições. Além disso, a transformação de Box-Cox (P = 0,353) e a transformação Johnson (P = 0,986) são eficazes na transformação dos dados para seguir uma distribuição normal.
Observação
Para várias distribuições, o Minitab também exibe resultados para a distribuição de um parâmetro adicional. Por exemplo, para a distribuição lognormal, o Minitab exibe resultados para ambas as versões de 2 parâmetros e de 3 parâmetros da distribuição. Para distribuições que tenham parâmetros adicionais, use o valor de p do teste da razão de verossimilhança (LRT P) para determinar se a adição de outro parâmetro melhora significativamente o ajuste da distribuição. Um valor de p de LRT que seja inferior a 0,05 indica que a melhoria no ajuste é significativa. Para obter mais informações, acesse Qualidade do ajuste para Identificação de distribuição individual e clique em "LRT P".
