Estimativas de máxima verossimilhança de parâmetros de distribuição
O método de máxima verossimilhança é usado para estimar os valores dos parâmetros de distribuição que maximizam a função de probabilidade para cada distribuição. O objetivo é obter o melhor "acordo" entre o modelo de distribuição e os dados de amostra observados.
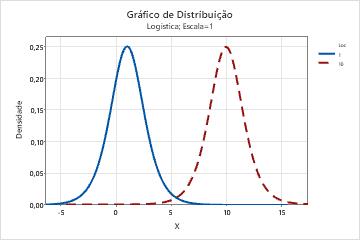
- Local
- Este parâmetro afeta o local de uma distribuição. Por exemplo, com
diferentes parâmetros de localização, uma distribuição logística pode ser
deslocada ao longo do eixo horizontal.
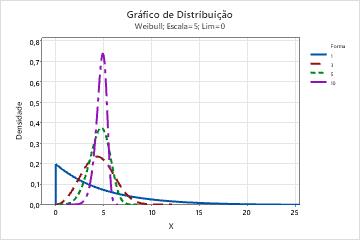
- Forma
- Este parâmetro afeta a forma da distribuição. Por exemplo, com diferentes
parâmetros de forma, uma distribuição Weibull pode parecer mais assimétrica
ou mais simétrica.
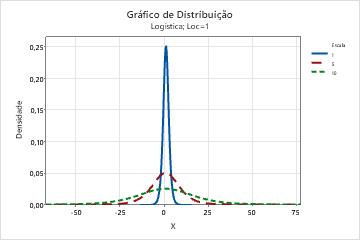
- Escala
- Este parâmetro afeta a escala da distribuição. Por exemplo, com parâmetros
de escala diferentes, uma distribuição logística pode parecer mais
"esticada" ou mais comprimida.
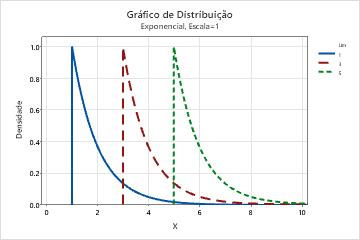
- Limite
- Este parâmetro afeta o valor mínimo de uma variável aleatória. Por exemplo,
com diferentes parâmetros de limite, é possível definir uma distribuição
exponencial ao longo de uma diferente gama de valores.
Observação
O Minitab calcula as estimativas dos parâmetros usando o método de máxima verossimilhança para todas as distribuições, exceto distribuições normais e lognormais que, em vez disso, usam estimativas não viciadas dos parâmetros.
Interpretação
Use as estimativas máxima verossimilhança dos parâmetros de distribuição para compreender o modelo de distribuição específico que é utilizado para seus dados. Por exemplo, suponha que um engenheiro de qualidade decide que, com base no conhecimento do processo histórico e do Anderson-Darling e nos valores de p de LRT, a distribuição Weibull para 3 parâmetros fornece o melhor ajuste para os dados do processo. Para compreender a distribuição de Weibull para 3 parâmetro específica que é usada para modelar os dados, o engenheiro examina as estimativas máxima verossimilhança quanto à forma, escala e limite que são calculados para a distribuição.
Distribuição
A identificação de distribuição individual fornece estatísticas de qualidade do ajuste e parâmetros de distribuição para várias distribuições comumente usadas. Muitas destas distribuições são versáteis e podem modelar uma variedade de dados contínuos, incluindo dados com valores positivos, valores negativos e 0.
- Lognormal para 2 parâmetros
- Exponencial com 1 parâmetros
- Weibull com 2 parâmetros
- Gama para 2 parâmetros
- Loglogística para 2 parâmetros
Portanto, se os dados contiverem valores negativos ou 0, o Minitab não relata resultados para estas distribuições específicas. Nesse caso, use os resultados para a versão de maior parâmetro de cada distribuição. Por exemplo, se os dados contiverem valores negativos, o Minitab não relata resultados para a distribuição lognormal para 2 parâmetros. Em vez disso, use os resultados para a distribuição lognormal de 3 parâmetros.
Para mais informações sobre as distribuições usadas na identificação de distribuição individual, acesse Por que a Weibull é a distribuição padrão para análise de capacidade não-normal?.
Observação
Para obter informações sobre as fórmulas usadas para calcular o FDP e FDA para cada distribuição, acesse Métodos e fórmulas para distribuições em Identificação de distribuição individual.
