N
O número de valores não faltantes na amostra. N é a contagem de todos os valores observados.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interpretação
Use N para avaliar o tamanho da amostra.
Importante
Tenha cuidado ao interpretar os resultados a partir de uma amostra muito pequena ou muito grande. Se você tem uma amostra muito pequena, um teste de qualidade de ajuste pode não ter poder suficiente para detectar desvios significativos da distribuição. Se você tem uma amostra muito grande, o teste pode ser tão poderosa a ponto de detectar até mesmo pequenos desvios da distribuição que não têm nenhuma significância prática. Além dos gráficos de probabilidade, utilize os valores de p para avaliar o ajuste de distribuição.
N*
Número de valores faltantes na amostra. N* é a contagem das células na worksheet que contêm o símbolo de valor faltante *.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Média
A média é calculada como a média dos dados, que é a soma de todas as observações divididas pelo número de observações.
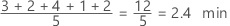
Interpretação
Use a média descreve para descrever a amostra com um único valor que representa o centro dos dados. Muitas análises estatísticas utilizam a média como um ponto de referência padrão.
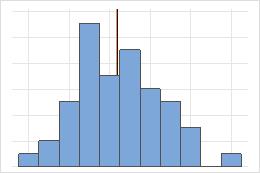
Média e mediana em uma distribuição simétrica
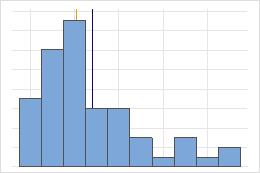
Média e mediana em uma distribuição não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são quase iguais. Portanto, as linhas se sobrepõem e não podem ser distinguidas uma da outra. Para a distribuição não simétrica, os dados são assimétricos à direita, o que faz com que o valor médio seja para maior do que a mediana.
StDev
O desvio padrão (StDev) é a medida mais comum de dispersão, ou o quanto os dados estão dispersos sobre a média. O símbolo σ (sigma) é frequentemente usado para representar o desvio padrão de uma população, e s é usado para representar o desvio padrão de uma amostra.
Interpretação
Use o desvio padrão para determinar o grau de dispersão dos dados a partir da média. A maior desvio padrão da amostra indica que os seus dados estão espalhados mais amplamente em torno da média.
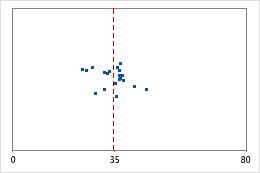
Hospital 1
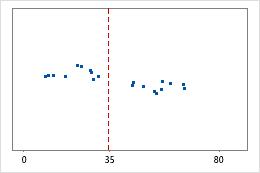
Hospital 2
Tempos de alta de hospital
Os administradores controlam o tempo gasto na alta de pacientes tratados nos departamentos de emergência de dois hospitais. Apesar de os tempos médios de alta serem quase os mesmos (35 minutos), os desvios padrão são significativamente diferentes. O desvio padrão do hospital 1 é de cerca de 6. Em média, o tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 6 minutos. O desvio padrão do hospital 2 é de cerca de 20. Na média, um tempo de alta de um paciente se desvia da média (linha tracejada) em cerca de 20 minutos.
Mediana
A mediana é o ponto médio do conjunto de dados. Este valor é o ponto médio em que metade das observações estão acima do valor e metade das observações estão abaixo do valor. A mediana é determinada por classificar as observações e encontrar a observação com o número [N + 1] / 2 na ordem de grandeza. Se o número de observações for par, a mediana é o valor entre as observações classificada com números de N / 2 e [N / 2] + 1.
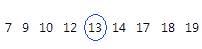
Para isso os dados ordenados, a mediana é 13. Isto é, metade dos valores é menor ou igual a 13, e a metade dos valores é maior ou igual a 13.
Interpretação

Média e mediana em uma distribuição simétrica

Média e mediana em uma distribuição não simétrica
Para a distribuição simétrica, a média (linha azul) e a mediana (linha laranja) são quase iguais. Portanto, as linhas se sobrepõem e não podem ser distinguidas uma da outra. Para a distribuição não simétrica, os dados são assimétricos à direita, o que faz com que o valor médio seja para maior do que a mediana.
Mínimo
O menor valor de dados.
Em nesses dados, o mínimo é 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o mínimo para identificar um possível outlier. Se o valor for anormalmente baixo, investigue suas possíveis causas, como um erro de entrada de dados ou um erro de medição.
Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo para avaliar sua amplitude. A amplitude é a diferença entre os valores máximo e mínimo no conjunto de dados. Quando você avalia a dispersão dos dados, também considera outras medidas, como o desvio padrão.
Máximo
O maior valor de dados.
Nesses dados, o máximo é 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretação
Use o máximo para identificar um possível outlier. Se o valor for anormalmente alto, investigue suas possíveis causas, como um erro de entrada de dados ou um erro de medição.
Uma das maneiras mais simples para avaliar a dispersão de seus dados é comparar o mínimo e o máximo para avaliar sua amplitude. A amplitude é a diferença entre o máximo e mínimo no conjunto de dados. Quando você avalia a dispersão dos dados, também considera outras medidas, como o desvio padrão.
Assimetria
A assimetria é a medida em que os dados não são simétricos.
Interpretação
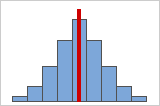
Figura A: Dados simétricos e distribuídos normalmente
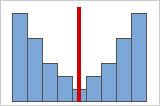
Figura B: Dados simétricos distribuídos não normalmente
Distribuições simétricas ou não assimétricas
Conforme os dados se tornam mais simétricos, seu valor se aproxima da assimetria 0. A Figura A mostra os dados distribuídos normalmente, o que, por definição, exibe relativamente pouca assimetria. A linha central do histograma de dados normais mostra que os dois lados refletem um ao outro. A falta de assimetria por si, contudo, não implica normalidade. A Figura B mostra uma distribuição onde os dois lados ainda refletem um ao outro, mas os dados não são normalmente distribuídos.
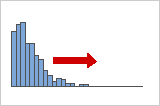
Distribuições com assimetria positiva ou à direita
Dados com assimetria positiva também são chamados de dados com assimetria à direita por causa da "cauda" dos pontos de distribuição para a direita. Os dados com assimetria positiva tem um valor de assimetria que é maior do que 0. Os dados salariais, muitas vezes, têm assimetria positiva: muitos funcionários ganham salários relativamente baixos, enquanto cada vez menos pessoas ganham salários muito altos.
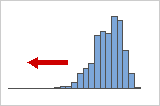
Distribuições com assimetria negativa ou à esquerda
Dados com assimetria negativa também são chamados de dados com assimetria à esquerda por causa da "cauda" dos pontos de distribuição para a esquerda. Os dados com assimetria negativa têm um valor de assimetria que é inferior a 0. Os dados taxa de falha é frequentemente assimetricamente negativo. Por exemplo, muito poucas lâmpadas queimam imediatamente, e a maioria das lâmpadas não queimam por um longo tempo.
Curtose
A curtose indica como as caudas de uma distribuição diferem da distribuição normal.
Interpretação
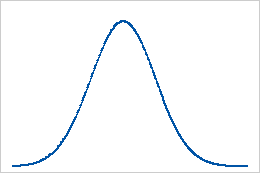
Linha de base: valor da curtose de 0
Os dados que seguem uma distribuição normal perfeitamente têm um valor de 0. Normalmente, os dados distribuídos estabelecem a linha de base para curtose. A curtose que se desvia significativamente de 0 pode indicar que os dados não estão normalmente distribuídos.
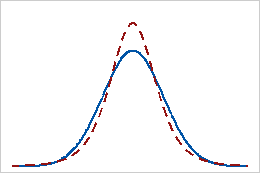
Curtose positiva
Uma distribuição com um valor de curtose positiva indica que a distribuição tem caudas mais pesadas do que a distribuição normal. Por exemplo, os dados que se seguem à distribuição T têm um valor de curtose positivo. A linha contínua mostra a distribuição normal e a linha pontilhada mostra uma distribuição T com uma curtose positiva.
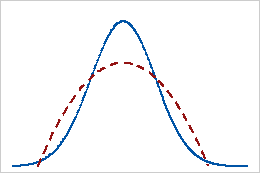
Curtose negativa
Uma distribuição que tem um valor de curtose negativo indica que a distribuição tem caudas mais leves do que a distribuição normal. Por exemplo, os dados que seguem uma distribuição beta com primeiro e segundo parâmetros de forma igual a 2 têm um valor de curtose negativo. A linha contínua mostra a distribuição normal e a linha pontilhada mostra uma distribuição beta com uma curtose negativa.
