Exemplo de Identificação de distribuição individual

Um engenheiro de qualidade de uma empresa suplementos nutricionais deseja avaliar o teor de cálcio em cápsulas de vitamina. O engenheiro coleta uma amostra aleatória de cápsulas e registra seu conteúdo de cálcio. Para determinar qual a análise estatística é apropriada para os dados, o engenheiro primeiro precisa determinar a distribuição dos dados.

O engenheiro realiza a identificação de distribuição individual para determinar qual distribuição melhor se ajusta aos dados.

Abra os dados amostrais, TeorDeCálcio.MTW.
Selecione Estat > Ferramentas da Qualidade > Identificação de distribuição individual.
Em Dados organizados como, selecione Coluna única, em seguida, insira Cálcio.
Em Tamanho do subgrupo, insira 1.
Clique em OK.

Interpretar os resultados

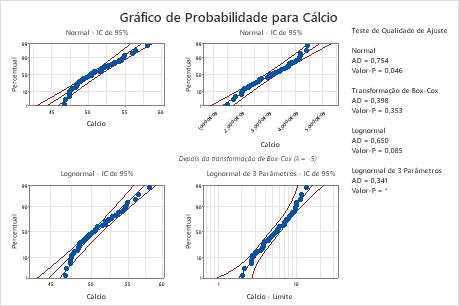
O Minitab exibe um gráfico de probabilidade e um valor de p para cada distribuição e transformação. Se uma distribuição for um bom ajuste para os dados (ou se for uma transformação efetiva), os pontos no gráfico seguem uma linha reta, dentro dos limites de confiança e o valor de p é maior do que o nível alfa. Um nível alfa de 0,05 é frequentemente utilizado. O valor de p para o teste de razão de verossimilhança (LRT) indica se a adição de um parâmetro adicional para uma distribuição melhora significativamente seu ajuste. Um valor de p de LRT que seja inferior a 0,05 indica que a melhoria é significativa.

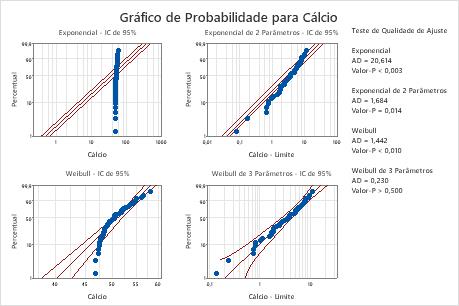
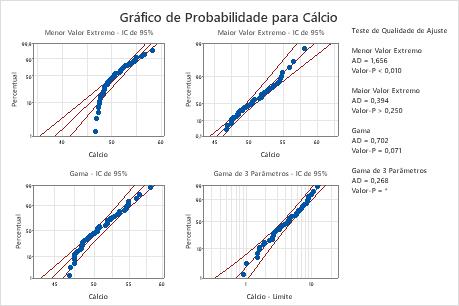
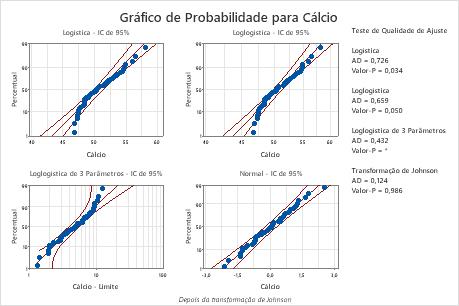
Para estes dados, a distribuição Weibull para 3 parâmetros (p > 0,500) e a distribuição do maior valor extremo (p > 0,250) são bons ajustes para os dados. A adição de um terceiro parâmetro melhora significativamente o ajuste da distribuição log-normal (LRT P = 0,017), a distribuição Weibull (LRT P = 0,000), a distribuição gama (LRT P = 0,006) e a distribuição loglogística (LRT P = 0,027).

A transformação de Box-Cox (p = 0,324) e a transformação Johnson (p = 0,986) são eficazes para estes dados. Após a transformação, a distribuição normal proporciona um bom ajuste para os valores transformados.

Exponencial de 2 Parâmetros

* AVISO * A matriz de variância/covariância dos parâmetros estimados não existe. O parâmetro
do limite é presumido como fixo para cálculos de intervalos de confiança.

Gama de 3 Parâmetros

* AVISO * A matriz de variância/covariância dos parâmetros estimados não existe. O parâmetro
do limite é presumido como fixo para cálculos de intervalos de confiança.

Distribuição	AD	P	TRV P
Normal	0,754	0,046
Transformação de Box-Cox	0,414	0,324
Lognormal	0,650	0,085
Lognormal de 3 Parâmetros	0,341	*	0,017
Exponencial	20,614	<0,003
Exponencial de 2 Parâmetros	1,684	0,014	0,000
Weibull	1,442	<0,010
Weibull de 3 Parâmetros	0,230	>0,500	0,000
Menor Valor Extremo	1,656	<0,010
Maior Valor Extremo	0,394	>0,250
Gama	0,702	0,071
Gama de 3 Parâmetros	0,268	*	0,006
Logística	0,726	0,034
Loglogística	0,659	0,050
Loglogística de 3 Parâmetros	0,432	*	0,027
Transformação de Johnson	0,124	0,986

Distribuição	Local	Forma	Escala	Limite
Normal*	50,78200		2,76477
Transformação de Box-Cox*	0,00000		0,00000
Lognormal*	3,92612		0,05368
Lognormal de 3 Parâmetros	1,69295		0,46849	44,74011
Exponencial			50,78200
Exponencial de 2 Parâmetros			4,06326	46,71873
Weibull		17,82470	52,13681
Weibull de 3 Parâmetros		1,47605	4,53647	46,66579
Menor Valor Extremo	52,22257		2,95894
Maior Valor Extremo	49,50370		2,16992
Gama		351,04421	0,14466
Gama de 3 Parâmetros		2,99218	1,63698	45,88376
Logística	50,57182		1,59483
Loglogística	3,92259		0,03121
Loglogística de 3 Parâmetros	1,54860		0,32763	45,46180
Transformação de Johnson*	0,02897		0,97293

Exemplo de Identificação de distribuição individual

Interpretar os resultados

Exponencial de 2 Parâmetros

Gama de 3 Parâmetros

Estatísticas Descritivas

Teste de Qualidade de Ajuste

Estimativas de MV dos Parâmetros da Distribuição