O que é % de tolerância?
Uma estatística que é diretamente afetada pelos limites de especificação é o % de tolerância estatística, que compara a tolerância com a variação do estudo. Idealmente, a tolerância deve amplamente abranger a variação do estudo, assegurando a variabilidade devido à medição R&R e à variação peça a peça, não empurre a saída do processo além dos limites de especificação.
Quando um processo tem dois limites de especificação, a tolerância é igual à diferença entre eles, e o % de tolerância é igual à variação do estudo de uma determinada fonte de variação dividida por esta tolerância. Contudo, este método é inválido quando você fornece um único limite de especificação.
Exemplo de processos com um limite de especificação
Muitos processos operam com apenas um limite de especificação. Por exemplo, uma serraria corta vigas para ficarem perfeitamente retas, mas as vigas frequentemente empenam durante a fabricação. As medições deste empenamento têm um limite superior de especificação para distinguir graus aceitáveis e não aceitáveis de empenamento. No entanto, essas medições não têm limite inferior de especificação porque não podem ter valores inferiores a zero. Na verdade, zero representa uma viga perfeitamente reta sem empenamento. Além disso, alguns processos têm um limite de especificação inferior, mas nenhum limite superior de especificação. Um fabricante de talheres deve verificar se a dureza de suas lâminas de faca é superior a 55 na escala C da Rockwell. O limite inferior de especificação é 55, mas não existe limite superior de especificação.
Como o Minitab calcula o % de tolerância quando eu insiro uma tolerância unilateral?
- O Minitab calcula uma variação do processo unilateral dividindo a estatística da variação do estudo por 2.
- O Minitab define a tolerância unilateral como o valor absoluto da diferença entre o limite de especificação único e o valor médio de todas as medições.
- O Minitab calcula a estatística do % de tolerância dividindo a variação do processo unilateral pela tolerância unilateral.

| Termo | Descrição |
|---|---|
| L | o limite de especificação único |
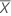 | a média de todas as observações |
Observação
Se a média de todas as observações for menor do que o limite inferior de especificação, ou maior do que o limite superior de especificação, as medições desviam fortemente de sua amplitude aceitável e o % de tolerância não é calculado.
