Neste tópico
Gráfico Vício versus Referência
Use o Gráfico Vício versus Referência para ver como os valores de vício variam para cada peça. Os pontos azuis representam os valores de vício para cada valor de referência. O quadrado vermelho representa o valor de vício médio para cada valor de referência. A linha é a linha de ajuste da regressão dos mínimos quadrados para a média dos desvios.
Interpretação
De maneira ideal, os desvios para cada peça são próximos a 0 e a linha ajustada é horizontal.
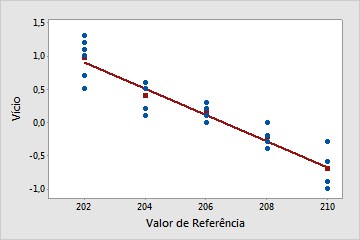
A linearidade parece ser um problema
A linha representada graficamente é inclinada. Neste exemplo, as medições para as peças menores são mais elevadas do que os seus valores para a peça de referência correspondente. As medições para peças maiores tendem a ser mais baixas do que os seus valores peça de referência correspondentes.
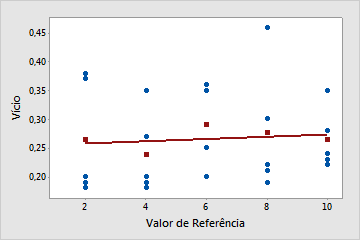
A linearidade não parece ser um problema
A linha representada graficamente está próxima da horizontal, o que indica que o vício médio é relativamente constante e não depende do valor de referência. Neste exemplo, as medições de todas as peças menores são mais elevadas do que os as medições da peça de referência correspondente.
Coef
Os coeficientes são números da linha de regressão do gráfico do valor Vício versus Referência.
A forma geral desta linha de regressão por mínimos quadrados é:
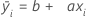
O termo, b, representa o coeficiente constante. Isso indica que a linha ajustada cruza o eixo y.
O termo, a, representa a o coeficiente angular. A inclinação de uma linha indica o declive da linha e representa a mudança no eixo-y sobre a mudança no eixo-x.
Interpretação
Quando o coeficiente angular, a, for muito pequeno, a inclinação está perto da horizontal. Assim, o vício é relativamente constante em toda os valores de referência, e a linearidade não é um problema significativo. Valores absolutos maiores do coeficiente angular, |a|, indicam um declive mais acentuado da linha. Se o valor de p da inclinação for inferior a alfa, a linearidade é significativa.
Na ausência de linearidade significativa, os valores absolutos maiores do coeficiente constante, |b|, indicam vício maior. Quando há linearidade significativa presente, devem ser observados os valores de vício individuais.
Coeficiente de SE
O erro padrão da estimativa de um coeficiente regressão mede o grau de precisão com que o modelo estima o valor desconhecido do coeficiente. O erro padrão do coeficiente é sempre positivo.
Interpretação
Use o erro padrão do coeficiente para medir a precisão da estimativa do coeficiente. Quando menor o erro padrão, mais precisa é a estimativa. Dividir o coeficiente pelo erro padrão calcula um valor t. Se o valor de p associado ao valor de t for menor que o nível de α, você conclui que o coeficiente é significativamente diferente de zero.
Valor de p para linearidade de medição
- P para Constante: use para testar se a constante da linha de linearidade for igual a 0.
- P para Inclinação: use para testar se a inclinação da linha de linearidade for igual a 0.
Interpretação
- Para a constante, se o valor-p for maior que o valor de α, você deixa de rejeitar a hipótese nula e conclui que o vício para todos os valores de referência é igual a 0.
- Para a inclinação, se o valor-p for maior do que o valor de α, você deixa de rejeitar a hipótese nula e conclui que o sistema de medição tem o mesma vício para todos os valores de referência (linearidade não está presente).
- Para a constante, se o valor-p for menor do que o valor α, rejeite a hipótese nula e conclua que o vício para todos os valores de referência não é igual a 0.
- Para a inclinação, se o valor-p for menor do que o valor de α, rejeite a hipótese nula e conclua que o sistema de medição não tem o mesmo vício para todos os valores de referência (linearidade está presente).
S e R-Sq
S e R-Sq (R2) são medidas de quão bem o modelo se ajusta aos dados.
S é uma estimativa de σ, o desvio padrão em torno da linha de regressão.
O R-Sq (R2) representa a porcentagem de variação no vício que é explicado pela relação linear entre as tendências e os valores de referência.
Interpretação
Valores menores de S indicam menor variabilidade nas estimativas de vício. R2 varia de 0 a 100%. Normalmente, quanto mais alto o valor de R2 melhor o modelo se ajusta aos seus dados.
Linearidade, %Linearity
A linearidade avalia a diferença no vício médio ao longo da amplitude operacional esperada do sistema de medição. Linearidade indica se o seu medidor tem a mesma precisão (o mesmo vício) em todos os valores de referência.
%Linearity é linearidade expressa como uma porcentagem da variação do processo.
Interpretação
Para interpretar a linearidade dos seus dados, determine se o vício muda entre os valores de referência. Se os dados não formarem uma linha horizontal em um gráfico de dispersão, a linearidade está presente. De maneira ideal, a linha ajustada será horizontal e estará próximo de 0.

A linearidade parece ser um problema
A linha representada graficamente é inclinada. Neste exemplo, as medições para as peças menores são mais elevadas do que os seus valores para a peça de referência correspondente. As medições para peças maiores tendem a ser mais baixas do que os seus valores peça de referência correspondentes.

A linearidade não parece ser um problema
A linha representada graficamente está próxima da horizontal, o que indica que o vício médio é relativamente constante e não depende do valor de referência. Neste exemplo, as medições de todas as peças menores são mais elevadas do que os as medições da peça de referência correspondente.
Para um medidor que mede de forma consistente as peças, %Linearity será próximo de 0.
Vício, %Bias
O vício é calculado como a diferença entre o valor padrão conhecido de uma peça de referência e a medição média observada.O vício é uma medida da precisão de um sistema de medição.
%Bias é o vício expresso como uma porcentagem da variabilidade do processo.
Interpretação
- Um vício positivo indica que o medidor mede alto.
- Um vício negativo indica que o medidor mede baixo.
Para um medidor que mede com precisão, o %bias é pequeno.
Valor de p para vício de medição
- P para o vício médio: use para testar se vício médio é igual a 0.
- P para cada valor de referência: use para testar se o vício é igual a 0 em cada valor de referência.
Interpretação
- Para cada valor de referência, se o valor de p for maior que o valor de α, você deixa de rejeitar a hipótese nula e conclui que o vício para todos os valores de referência é igual a 0.
- Para o vício médio, se o valor de p for maior que o valor de α, você deixa de rejeitar a hipótese nula e conclui que o vício médio é igual a 0.
- Para cada valor de referência, se o valor de p for menor do que o valor α, rejeite a hipótese nula e conclua que o vício para todos os valores de referência não é igual a 0.
- Para o vício médio, se o valor de p for menor do que o valor α, rejeite a hipótese nula e conclua que o vício médio não é igual a 0.
