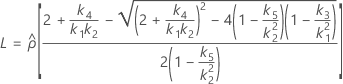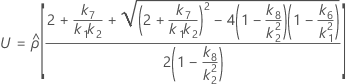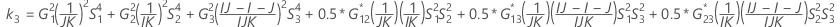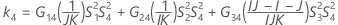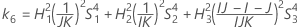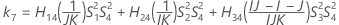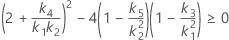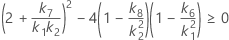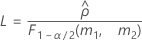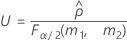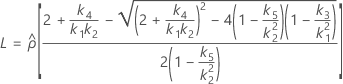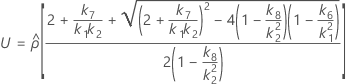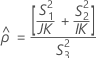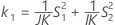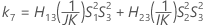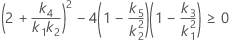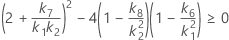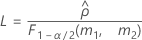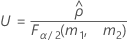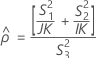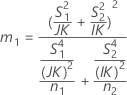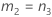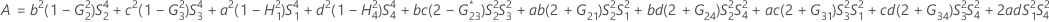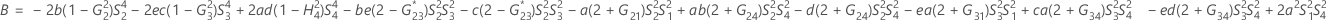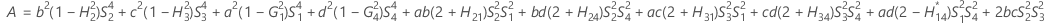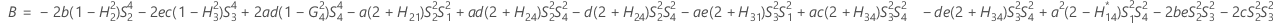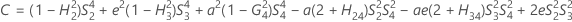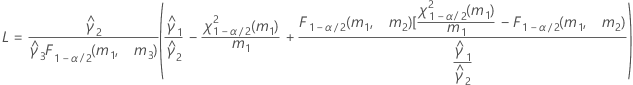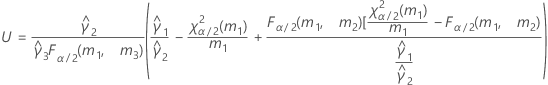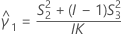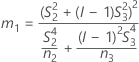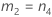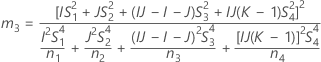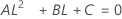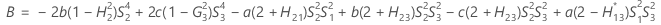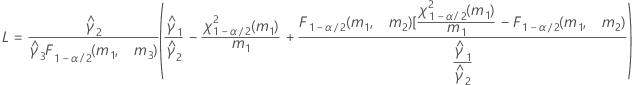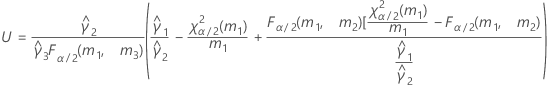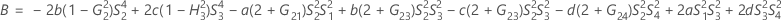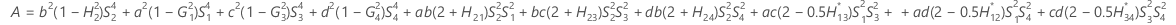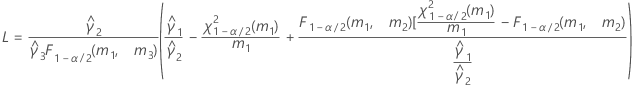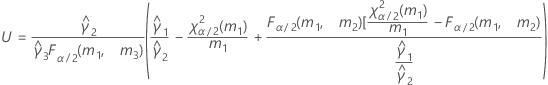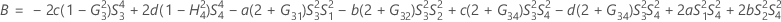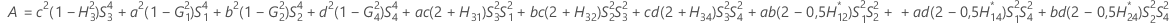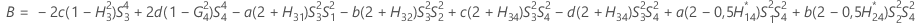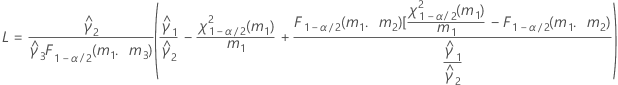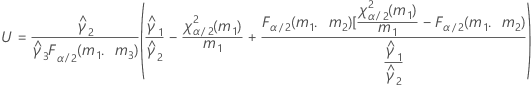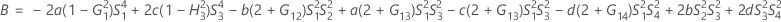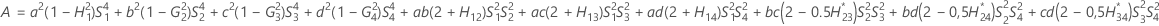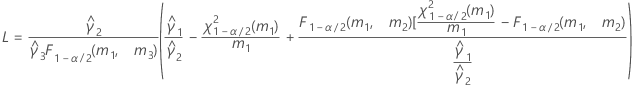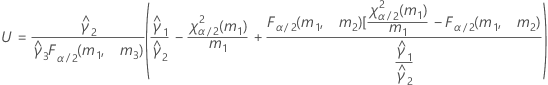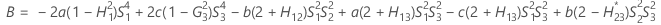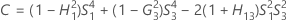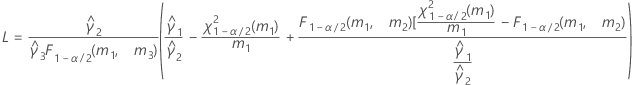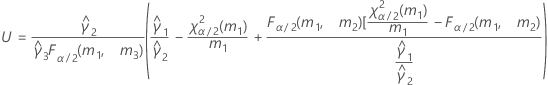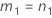Neste tópico
- Intervalo de confiança para a proporção de variância e a variância total
- Intervalo de confiança para a razão de variância de reprodutibilidade e a variância total
- Intervalo de confiança para a proporção de variância do operador e a variância total
- Intervalo de confiança para a proporção de variância de interação e a variância total
- Intervalo de confiança para a proporção de variância da peça e a variância total
- Intervalo de confiança para a proporção de variância da medição e a variância total
Intervalo de confiança para a proporção de variância e a variância total
Com operador
Quando o operador e o termo de interação estão incluídos, existem dois métodos de cálculo possíveis. Em primeiro lugar, o Minitab calcula os limites usando o método modificado de grande amostra (MLS). Se certas condições não forem atendidas durante os cálculos, o Minitab usa aproximação de Satterthwaite. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
- Método MLS
-

- Aproximação de Satterthwaite
- As fórmulas para os limites inferiores e superiores ainda se mantêm, a não ser que L e U sejam definidos como a seguir:
Sem termo do operador
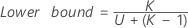

Sem termo de interação
Quando o operador e o termo de interação estão incluídos, existem dois métodos de cálculo possíveis. Em primeiro lugar, o Minitab calcula os limites usando o método modificado de grande amostra (MLS). Se certas condições não forem atendidas durante os cálculos, o Minitab usa aproximação de Satterthwaite. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
- Método MLS
-
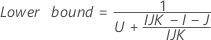
- Aproximação de Satterthwaite
- As fórmulas para os limites inferiores e superiores ainda se mantêm, a não ser que L e U sejam definidos como a seguir:
Notação
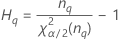
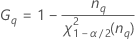
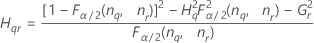
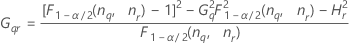
| Termo | Descrição |
|---|---|
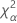 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança para a razão de variância de reprodutibilidade e a variância total
Com termo de interação
Há dois métodos possíveis de cálculo. Em primeiro lugar, o Minitab calcula os limites usando o método modificado de grande amostra (MLS). Se certas condições não forem atendidas durante os cálculos, o Minitab usa uma aproximação alternativa. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
- Método MLS
- Os limites inferior e superior para um intervalo de confiança aproximado de (1 - α) * 100% são calculados através da resolução de equações do segundo grau.
- Segundo método
- Os limites inferior e superior para um intervalo de confiança aproximado (1-α) * 100% são calculados como se segue:
Sem termo de interação
Há dois métodos possíveis de cálculo. Em primeiro lugar, o Minitab calcula os limites usando o método modificado de grande amostra (MLS). Se certas condições não forem atendidas durante os cálculos, o Minitab usa uma aproximação alternativa. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
- Método MLS
- Os limites inferior e superior para um intervalo de confiança aproximado de (1 - α) * 100% são calculados através da resolução de equações do segundo grau. Limite inferior, L, é igual a J vezes a menor solução com a equação a seguir.
- Segundo método
- Os limites inferior e superior para um intervalo de confiança aproximado (1-α) * 100% são calculados como se segue:
Notação
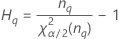
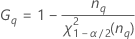
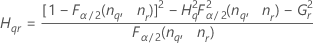
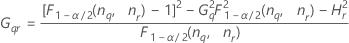
| Termo | Descrição |
|---|---|
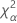 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
| a | I |
| b | J |
| c | (IJ – I –J) |
| d | IJ(K-1) |
| e | I – 1 |
Intervalo de confiança para a proporção de variância do operador e a variância total
Há dois métodos possíveis de cálculo. Em primeiro lugar, o Minitab calcula os limites usando o método modificado de grande amostra (MLS). Se certas condições não forem atendidas durante os cálculos, o Minitab usa uma aproximação alternativa. Para calcular os limites de confiança de um lado, substitua α/2 por α em H e G.
- Método MLS
- Os limites inferior e superior para um intervalo de confiança aproximado de (1 - α) * 100% são calculados através da resolução de equações do segundo grau.
- Segundo método
- Os limites inferior e superior para um intervalo de confiança aproximado (1-α) * 100% são calculados como se segue:
Notação
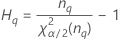
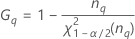
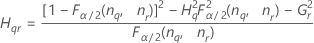
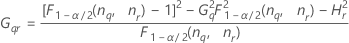
| Termo | Descrição |
|---|---|
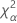 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança para a proporção de variância de interação e a variância total
Há dois métodos possíveis de cálculo. Em primeiro lugar, o Minitab calcula os limites usando o método modificado de grande amostra (MLS). Se certas condições não forem atendidas durante os cálculos, o Minitab usa uma aproximação alternativa. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
- Método MLS
- Os limites inferior e superior para um intervalo de confiança aproximado de (1 - α) * 100% são calculados através da resolução de equações do segundo grau.
- Segundo método
- Os limites inferior e superior para um intervalo de confiança aproximado (1-α) * 100% são calculados como se segue:
Notação
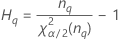
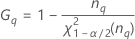
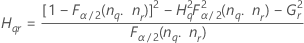
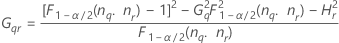
| Termo | Descrição |
|---|---|
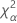 | o percentil α *100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança para a proporção de variância da peça e a variância total
Com termo de interação e do operador
Há dois métodos possíveis de cálculo. Em primeiro lugar, o Minitab calcula os limites usando o método modificado de grande amostra (MLS). Se certas condições não forem atendidas durante os cálculos, o Minitab usa uma aproximação alternativa. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
- Método MLS
- Os limites inferior e superior para um intervalo de confiança aproximado de (1 - α) * 100% são calculados através da resolução de equações do segundo grau.
- Segundo método
- Os limites inferior e superior para um intervalo de confiança aproximado (1-α) * 100% são calculados como se segue:
Sem termo do operador
Limite inferior = 1 - (limite inferior para a razão da variância da repetibilidade e a variância total)
Limite superior = 1 - (limite superior para a razão de variância da repetibilidade e a variância total)
Sem termo de interação
- Método MLS
- Os limites inferior e superior para um intervalo de confiança aproximado de (1 - α) * 100% são calculados através da resolução de equações do segundo grau.
- Segundo método
- Os limites inferior e superior para um intervalo de confiança aproximado (1-α) * 100% são calculados como se segue:
Notação
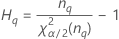
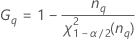
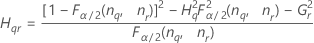
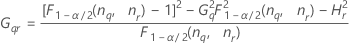
| Termo | Descrição |
|---|---|
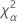 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança para a proporção de variância da medição e a variância total
Limite inferior = 1 - (limite inferior do IC para a proporção de variância parte e a variância total)
Limite superior = 1 - (limite superior do IC para a proporção de variância parte e a variância total)