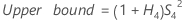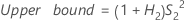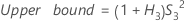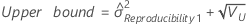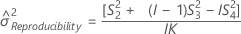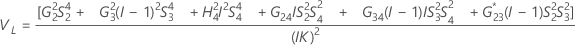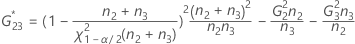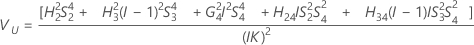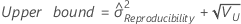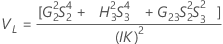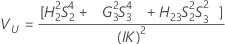Neste tópico
- Notações comuns e regras para intervalos de confiança de medições R&R
- Intervalo de confiança de componentes de variância de repetibilidade
- Intervalo de confiança de componentes de variância da reprodutibilidade (ou operador)
- Intervalo de confiança de componentes de variância do operador
- Intervalo de confiança de componentes de variância da interação
- Intervalo de confiança de componentes de variância total do medidor
- Intervalo de confiança de componentes de variância peça a peça
- Intervalo de confiança de componentes de variância total
Notações comuns e regras para intervalos de confiança de medições R&R
Para todos os componentes de variância, os limites inferiores e superiores para componentes de variância não devem ser valores negativos. Se os limites calculados usando as fórmulas forem negativos, eles são definidos como zero.
Para todas as relações entre 0 e 1, os limites inferior e superior também devem estar entre 0 e 1. Se os limites estiverem fora do intervalo, eles são definidos para 0 ou 1 em conformidade.
Notação
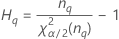
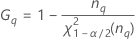
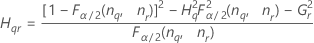
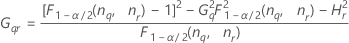
| Termo | Descrição |
|---|---|
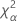 | o percentil α *100 da distribuição qui-quadrado com nq graus de liberdade |
| Fα(nq, nγ) | o percentil α * 100 da distribuição F com nq e nγ graus de liberdade |
| I | o número de peças |
| J | o número de operadores |
| K | o número de réplicas |
Para os graus de liberdade
Peças: n1=I-1
Operadores: n2=J-1
Peças*Operadores: n3=(I-1)(J-1)
Réplicas: n4=IJ(K–1)
MSPart= S12
MSOperador = S22
MSPeça*Operador = S32
MSRéplicas = S42
Intervalo de confiança de componentes de variância de repetibilidade
O Minitab calcula os limites inferior e superior para um intervalo de confiança exato de (1-α) * 100%. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
Fórmulas
- Com operador
-
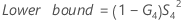
- Sem operador
-

- Sem termo de interação
-

Notação
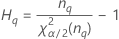
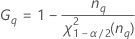
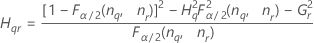
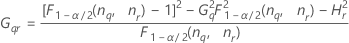
| Termo | Descrição |
|---|---|
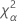 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança de componentes de variância da reprodutibilidade (ou operador)
O Minitab usa o método modificado de grande amostra (MLS) para calcular os limites inferior e superior para um valor aproximado (1 - α) * intervalo de confiança de 100%. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
Fórmulas
- Com termo de interação
-
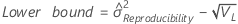
- Sem termo de interação
-
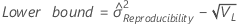
Notação
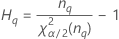
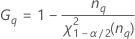
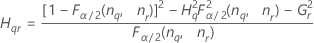
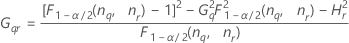
| Termo | Descrição |
|---|---|
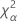 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança de componentes de variância do operador
O Minitab usa o método modificado de grande amostra (MLS) para calcular os limites inferior e superior para um valor aproximado (1 - α) * intervalo de confiança de 100%. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
Fórmulas


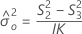
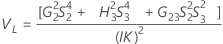
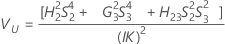
Notação
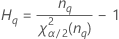
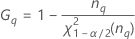
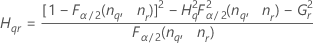
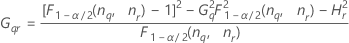
| Termo | Descrição |
|---|---|
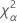 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança de componentes de variância da interação
O Minitab usa o método modificado de grande amostra (MLS) para calcular os limites inferior e superior para um valor aproximado (1 - α) * intervalo de confiança de 100%. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
Fórmulas


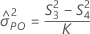

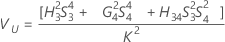
Notação
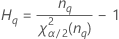
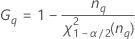
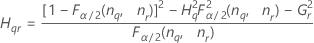
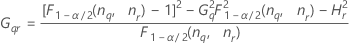
| Termo | Descrição |
|---|---|
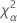 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança de componentes de variância total do medidor
Com termo de interação e do operador
O Minitab usa o método modificado de grande amostra (MLS) para calcular os limites inferior e superior para um valor aproximado (1 - α) * intervalo de confiança de 100%. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.



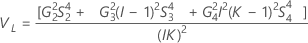
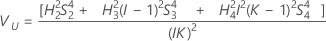
Sem termo do operador
Os limites inferior e superior para um intervalo de confiança exato de (1-α) * 100% são:


Sem termo de interação
O Minitab usa o método modificado de grande amostra (MLS), os limites inferior e superior para um valor aproximado (1 - α) * intervalo de confiança de 100%. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.


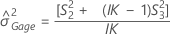
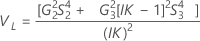
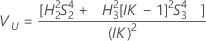
Notação
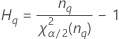
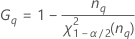
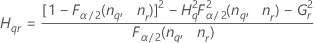
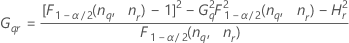
| Termo | Descrição |
|---|---|
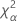 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança de componentes de variância peça a peça
O Minitab usa o método modificado de grande amostra (MLS) para calcular os limites inferior e superior para um valor aproximado (1 - α) * intervalo de confiança de 100%. Para calcular os limites de confiança unilateral, substitua α/2 por α em H e G.
Com operador



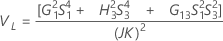
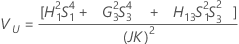
Sem operador


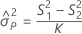
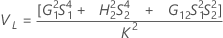
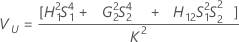
Sem interação



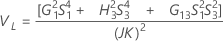
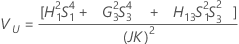
Notação
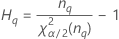
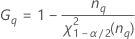
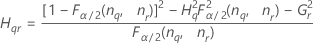
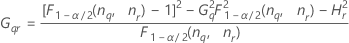
| Termo | Descrição |
|---|---|
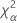 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |
Intervalo de confiança de componentes de variância total
O Minitab usa o método modificado de grande amostra (MLS) para calcular os limites inferior e superior para um valor aproximado (1 - α) * intervalo de confiança de 100%. Para calcular os limites de confiança unilateral , substitua α/2 por α em H e G.
Com operador



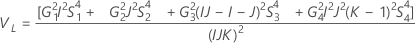
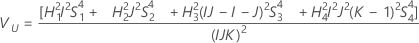
Sem operador


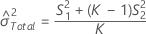
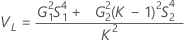
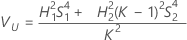
Sem termo de interação


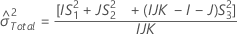
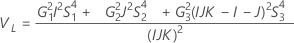
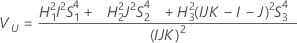
Notação
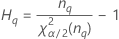
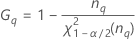
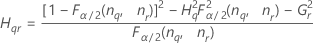
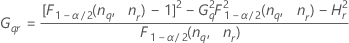
| Termo | Descrição |
|---|---|
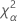 | o percentil α * 100 da distribuição qui-quadrado com nq graus de liberdade |
| J | o número de operadores |
| I | o número de peças |
| K | o número de réplicas |