Neste tópico
DF
Os graus de liberdade (DF) para cada SS (soma dos quadrados). Em geral, DF mede quanta informação está disponível para calcular cada SS.
SS
A soma dos quadrados (SS) é a soma das distâncias ao quadrado, e é uma medida da variabilidade que é a partir de diferentes fontes. O SS total indica a quantidade de variabilidade dos dados a partir da média global. O SS do operador indica a quantidade de variabilidade entre a medição média para cada operador e a média geral.
SS Total = SS Peça + SS Operador + SS Operador * Peça + SS Repetibilidade
MS
Os quadrados médios (MS) representam a variabilidade nos dados provenientes de diferentes fontes. MS é responsável pelo fato de que diferentes fontes apresentam diferentes números de níveis ou valores possíveis.
MS = SS/DF para cada fonte de variabilidade
F
A estatística F é utilizada para determinar se os efeitos do Operador, Peça, ou Operador*Peça são estatisticamente significativos.
Quanto maior for a estatística F, mais provável é que o fator contribua de forma significativa para a variabilidade na resposta variável ou medição.
P
O valor-p é a probabilidade de se obter uma estatística de teste (como a estatística F) que seja pelo menos tão extrema quanto o valor que é calculado a partir da amostra, se a hipótese nula for verdadeira.
Interpretação
Utilizar o valor-p na tabela ANOVA para determinar se as medições médias são significativamente diferentes. O Minitab exibe uma tabela ANOVA apenas se você selecionar a opção de ANOVA para Método de Análise.
Um valor de p baixo indica que a suposição de que todas as peças, operadores ou interações que compartilham a mesma média provavelmente não é verdadeira.
- Valor-p ≤ α: pelo menos uma média é estatisticamente diferente
- Se o valor-p for menor ou igual ao nível de significância, rejeite a hipótese nula e conclua que, pelo menos, uma das médias é significativamente diferente das outras. Por exemplo, pelo menos um operador mede de maneira diferente.
- Valor-p > α: as médias não são significativamente diferentes
- Se o valor-p for maior do que o nível de significância, você não deve rejeitar a hipótese nula porque não há evidências suficientes para concluir que as médias da população são diferentes. Por exemplo, não é possível concluir que os operadores medem de forma diferente.
VarComp
VarComp são os componentes de variância de cada fonte da tabela ANOVA.
Interpretação
Use os componentes de variância para avaliar a variação de cada fonte de erros de medição.
Em um sistema de medição aceitável, o maior componente de variação é variação peça a peça. Se repetibilidade e reprodutibilidade contribuir em grandes quantidades para a variação, será necessário investigar a origem do problema e tomar ações corretivas.
%Contribution (of VarComp)
% de contribuição é o percentual de variação global de cada componente de variância. É calculado como o componente de variância para cada fonte dividida pela variação total, e então multiplicado por 100 para se expressar como uma porcentagem.
Interpretação
Use o %Contribution para avaliar a variação de cada fonte de erros de medição.
Em um sistema de medição aceitável, o maior componente de variação é variação peça a peça. Se repetibilidade e reprodutibilidade contribuir em grandes quantidades para a variação, será necessário investigar a origem do problema e tomar ações corretivas.
StdDev (SD)
StdDev (SD) é o desvio padrão para cada fonte de variação. O desvio padrão é igual à raiz quadrada do componente de variância para essa fonte.
O desvio padrão é uma medida conveniente de variação porque tem as mesmas unidades que as medidas e tolerância da peça.
Variação de Estudo (6 * SD)
A variação estudo é calculada como o desvio padrão para cada fonte de variação multiplicada por 6 ou o multiplicador que você especificar em Variação do estudo.
Normalmente, a variação do processo é definida como 6s, onde s é o desvio padrão como uma estimativa do desvio padrão da população (denotada por σ ou Sigma). Quando os dados são distribuídos normalmente, cerca de 99,73% dos dados caem dentro de 6 desvios padrão da média. Para definir um percentual diferente de dados, use outro multiplicador de desvio padrão. Por exemplo, se você quer saber, onde 99% dos dados caem, você usa um multiplicador de 5,15, em vez do multiplicador padrão de 6.
%Study Var (%SV)
A variação de %study é calculada como a variação de estudo para cada fonte de variação, dividida pela variação total e multiplicada por 100.
%Study Var é a raiz quadrada do componente de variância calculado (VarComp) para aquela fonte. Portanto, os valores de %Contribution de VarComp somam 100, mas os valores de %Study Var não.
Interpretação
Use %Study Var para comparar a variação sistema de medição para a variação total. Se você usar o sistema de medição para avaliar melhorias de processos, como redução da variação peça a peça, %Study Var é a melhor estimativa da precisão de medição. Se você quiser avaliar a capacidade do sistema de medição para avaliar peças em comparação com especificação, %Tolerance é a métrica adequada.
%Tolerance (SV/Toler)
O %Tolerance é calculado como a variação do estudo para cada fonte, dividida pela tolerância do processo e multiplicada por 100.
Se houver tolerância, o Minitab calcula a %Tolerance, que compara a variação do sistema de medição com as especificações.
Interpretação
Use %Tolerance para avaliar peças em relação às especificações. Se você usar o sistema de medição para melhoria de processos, como a redução da variação peça a peça, %variável do estudo é a métrica adequada.
%Process (SV/Proc)
Se você inserir um desvio padrão histórico, mas usar as peças no estudo para estimar a variação do processo, o Minitab calcula o %Process. O %Process compara a variação do sistema de medição com a variação do processo histórico. O %Process é calculado como a variação de estudo para cada fonte, dividida pela variação do processo histórico e multiplicada por 100. Por padrão, a variação do processo é igual a 6 vezes o desvio padrão histórico.
Se você usar um desvio padrão histórico para estimar a variação do processo, o Minitab não mostra %Process porque %Process é idêntico a %Study Var.
IC de 95%
Intervalos de confiança de 95% (IC de 95%) são intervalos de valores propensos a conter o verdadeiro valor de cada métrica de erro de medição.
O Minitab fornece intervalos de confiança para os componentes de variância, o % de contribuição dos componentes de variância, o desvio padrão, a variação do estudo, o % de variação estudo, o % de tolerância, e o número de categorias distintas.
Interpretação
Como as amostras de dados são aleatórias, não é provável que dois estudos de medição produzam intervalos de confiança idênticos. Mas, se você repetir seus estudos muitas vezes, uma certa porcentagem dos intervalos de confiança resultantes contém o erro de medição verdadeiro desconhecido. A porcentagem destes intervalos de confiança que contém o parâmetro é o nível de confiança do intervalo.
Por exemplo, com um nível de confiança de 95%, é possível ter 95% de certeza de que o intervalo de confiança contém o valor verdadeiro. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança incluir valores que tenham significância prática para a sua situação. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
Suponha que VarComp para repetibilidade seja 0,044727 e o IC correspondente a 95% é (0,035, 0,060). A estimativa de variação para a repetibilidade é calculada a partir dos dados para 0,044727. É possível ter 95% de certeza de que o intervalo de 0,035 a 0,060 contém a verdadeira variação para a repetibilidade.
Número de categorias distintas
O número de categorias distintas é uma métrica utilizada em estudos de medição R&R para identificar a capacidade de um sistema de medição para detectar uma diferença na característica medida. O número de categorias distintas representa o número de intervalos de confiança não sobrepostos que abrangem a gama de variação do produto, como definido pelas amostras que você escolheu. O número de categorias distintas também representa o número de grupos dentro de seus dados do processo que o seu sistema de medição é capaz discernir.
Interpretação
O Manual de Análise de Sistemas de Medição1 publicado pelo Automobile Industry Action Group (AIAG), afirma que cinco categorias ou mais indicam um sistema de medição aceitável. Se o número de categorias distintas for inferior a cinco, o sistema de medição pode não apresentar resolução suficiente.
Normalmente, quando o número de categorias distintas é inferior a dois, o sistema de medição não tem valor para controlar o processo, porque não é possível fazer distinção entre as peças. Quando o número de categorias distintas é dois, é possível dividir as peças em apenas dois grupos, como alto e baixo. Quando o número de categorias distintas é três, é possível dividir as peças em três grupos, como baixo, médio e alto.
Para obter mais informações, vá para Como usar o número de categorias distintas.
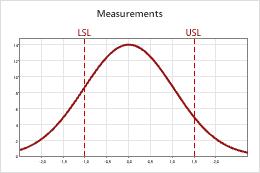
Probabilidades de erros de classificação
Quando você determina pelo menos um limite de especificação, o Minitab pode calcular as probabilidades de falsa resposta do produto. Devido a esta variação de medidor, o valor medido da peça não é sempre igual ao valor verdadeiro desta peça. A discrepância entre o valor medido e o valor real cria o potencial para erro na classificação das peças.
- Probabilidade conjunta
- Use a probabilidade conjunta quando não tiver conhecimento anterior sobre a aceitabilidade das peças. Por exemplo, você está coletando amostras da linha e não sabe se cada peça em particular é boa ou ruim. Há dois erros de classificação que podem ser cometidos:
- A probabilidade de que a peça seja ruim e que você a aceite.
- A probabilidade de que a peça seja boa e você a rejeite.
- Probabilidade condicional
- Use a probabilidade condicional quando você tiver conhecimento anterior sobre a aceitabilidade das peças. Por exemplo, você está coletando amostras de uma pilha de retrabalho ou de uma pilha de produtos que em breve serão enviados como bons. Há dois erros de classificação que podem ser cometidos:
- A probabilidade de que você aceitar uma peça que tenha sido amostrada de uma pilha de produtos ruins que precisam ser retrabalhados (também chamada de falso aceite).
- A probabilidade de você rejeitar uma peça que foi amostrada de uma pilha produtos bons que estão prestes a serem enviados (também chamado de falsa rejeição).
Interpretação
Probabilidade Conjunta
| Descrição | Probabilidade |
|---|---|
| Uma parte selecionada aleatoriamente é inválida, mas foi aceita | 0,037 |
| Uma parte selecionada aleatoriamente é válida, mas foi rejeitada | 0,055 |
Probabilidade Condicional
| Descrição | Probabilidade |
|---|---|
| Uma parte de um grupo de produtos inválidos foi aceita | 0,151 |
| Uma parte de um grupo de produtos válidos foi rejeitada | 0,073 |
A probabilidade conjunta de que uma peça seja ruim e você a aceite é 0,037. A probabilidade conjunta que uma peça seja boa e você a rejeite é 0,055.
A probabilidade condicional de um falso aceite, que você aceite uma peça durante a reinspeção quando ela realmente está fora da especificação, é 0,151. A probabilidade condicional de uma falsa rejeição, que você rejeite uma peça durante a reinspeção quando ela realmente está dentro da especificação, é 0,073.
VDA 5
Observação
O VDA 5 está disponível apenas no aplicativo web.
Observação
A análise usa a incerteza máxima entre uEVR, uRE e uEVO para calcular a variação do processo de medição. A % do total para as outras 2 estatísticas está ausente porque essas estatísticas não contribuem para o total.
- Calibração (uCAL)
- Calibração (uCAL) é a incerteza nas medições da calibração do padrão de referência. Essa estatística é uma entrada para a análise. Normalmente, esse valor vem do certificado de calibração.
- Repetibilidade na referência (uEVR)
- A repetibilidade na referência (uEVR) é a incerteza de medições repetidas da peça de referência pelo mesmo operador com o mesmo dispositivo. Essa estatística é uma entrada para a análise. Normalmente, esse valor vem de um estudo de medição Tipo I.
- Resolução (uRE)
- Resolução (uRE) é a incerteza devido à resolução do medidor. A análise calcula essa estatística quando a resolução do medidor é uma entrada para a análise.
- Repetibilidade do objeto medido (uEVO)
- A repetibilidade do objeto medido (uEVO) é a incerteza devido à repetibilidade no estudo Gage R&R. Repetibilidade é a variabilidade nas medições quando o mesmo operador mede a mesma peça várias vezes.
- Viés (uBI)
- Viés (uBI) é a incerteza nas medições devido à diferença da medida de referência conhecida e da média das medições no estudo. Essa estatística é uma entrada para a análise. Normalmente, esse valor vem de um estudo de viés em que a peça de referência está dentro da faixa de medições.
- Linearidade (uLIN)
- Linearidade (uLIN) é a incerteza nas medições da linearidade. A linearidade é a diferença entre o valor da peça de referência e a medida média que vem da mudança no viés à medida que o valor da peça muda. Essa estatística é uma entrada para a análise. Normalmente, esse valor vem de um estudo de linearidade em que a peça de referência estava dentro da faixa de medições.
- Outros fatores (uREST)
- Outros fatores (uREST) é a incerteza nas medições devido a um ou mais fatores adicionais. Se as especificações para a análise tiverem um fator adicional, essa incerteza será uma entrada para a análise. Se as especificações para a análise tiverem mais de um fator, essa incerteza combinará os valores. Por exemplo, use as especificações de outros fatores para levar em conta a incerteza devido à temperatura se as medições tiverem diferenças maiores quando a coleta de dados estiver em uma temperatura mais alta.
- Operadoras (uAV)
- Operadores (uAV) é a incerteza nas medições devido à reprodutibilidade no estudo Gage R&R. A reprodutibilidade é a variabilidade nas medições quando diferentes operadores medem a mesma peça.
- Interações (uIA)
- Interações (uIA) é a incerteza nas medições devido à interação entre a peça e o operador no Estudo de Medição R&R. A interação está na análise quando a interação Parte*Operador é estatisticamente significativa na tabela ANOVA.
- Processo de medição (uMP)
- O processo de medição (uMP) combina todos os componentes de incerteza para estimar a incerteza total do processo de medição.
- % do Total
- Para cada fonte de incerteza, a análise apresenta a porcentagem do uMP que resulta dessa fonte. Use a porcentagem para comparar a quantidade de incerteza das diferentes fontes.
- % de tolerância (%QMP)
- % de tolerância (%QMP) combina a incerteza do processo de medição com a variação do estudo e compara o valor com a tolerância do processo. %QMP é uma maneira comum de decidir se um processo de medição é satisfatório. Em algumas aplicações, um valor de 30% ou menos indica que um processo de medição é satisfatório.
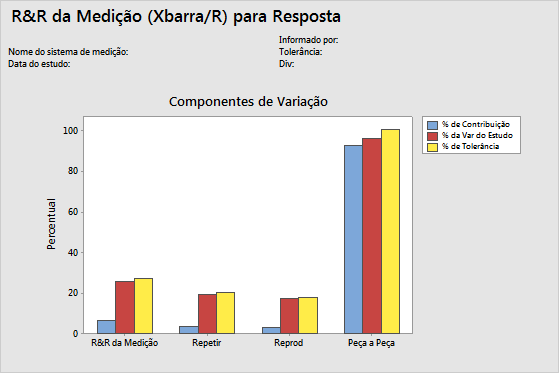
Gráfico dos componentes da variação
Os componentes do gráfico de variação são um resumo gráfico dos resultados de um estudo de medição R&R.
- Medição R&R total: a variabilidade do sistema de medição que inclui vários operadores que utilizam a mesma medição.
- Repetibilidade: a variabilidade nas medições quando o mesmo operador mede a mesma peça várias vezes.
- Reprodutibilidade: a variabilidade nas medições quando diferentes operadores medem a mesma peça.
- Peça a peça: a variabilidade nas medições devida às diferentes peças.
Interpretação
- %Contribution
- %Contribution é o percentual de variação global de cada componente de variância. É calculado como o componente de variância para cada fonte dividida pela variação total, e então multiplicado por 100.
- Variação de %Study
- A variação de %Study representa a porcentagem de variação do estudo de cada fonte. É calculado como a variação de estudo para cada fonte dividida pela variação total do estudo e, em seguida, multiplicado por 100.
- %Tolerance
- %Tolerance compara a variação sistema de medição com as especificações. É calculado como a variação do estudo para cada fonte, dividido pela tolerância do processo e, em seguida, multiplicado por 100.
- %Process
- O %Process compara a variação do sistema de medição com a variação total. É calculado como a variação de estudo para cada fonte dividido pela variação do processo histórico e, em seguida, multiplicado por 100.
Em um sistema de medição aceitável, o maior componente de variação é variação peça a peça.
Carta R
A carta R é uma carta de controle de amplitudes que exibe a consistência do operador.
- Pontos representados graficamente
- Para cada operador, a diferença entre a maior e a menor medições de cada peça. A carta R representa graficamente os pontos por operador, de forma que você pode ver quão consistente cada operador é.
- Linha central (Rbarra)
- A média global do processo (isto é, média de todos os intervalos de amostras).
- Limites de controle (LIC e LSC)
- A quantidade de variação que pode ser esperada para os intervalos de amostras. Para calcular os limites de controle, o Minitab usa a variação dentro de amostras.
Observação
Se cada operador mede cada peça 9 vezes ou mais, o Minitab exibe uma carta S em vez de uma carta R.
Interpretação
Uma pequena amplitude média indica que o sistema de medição tem baixa variação. Um ponto que é maior do que o limite superior de controle (LSC) indica que o operador não mede as peças consistentemente. O cálculo do LSC inclui o número de medições por peça para cada operador, e a variação peça a peça. Se os operadores medirem peças consistentemente, a amplitude entre as medições maior e menor será pequena em relação à variação do estudo, e os pontos devem estar sob controle.
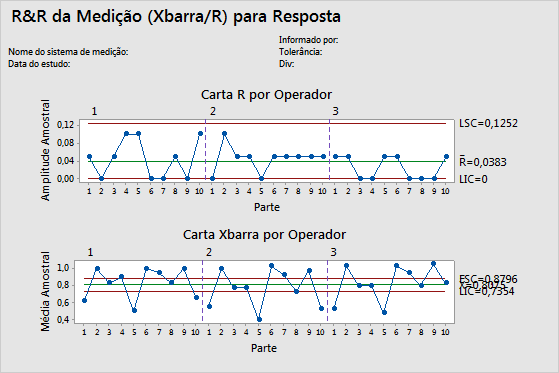
Carta Xbarra
A carta Xbarra compara a variação entre peças com o componentes de repetibilidade.
- Pontos representados graficamente
- A medição média de cada peça, representada graficamente por cada operador.
- Linha central (Xbarra)
- A média geral de todas as medições de peças aferidas por todos os operadores.
- Limites de controle (LIC e LSC)
- Os limites de controle estão baseados na estimativa de repetibilidade e no número de medições em cada média.
Interpretação
As peças selecionadas para um estudo de medição R&R devem representar toda a variedade de peças possível. Assim, este gráfico deve indicar mais variação entre as médias de peças do que o que se espera apenas da variação repetibilidade.
De maneira ideal, o gráfico tem limites de controle estreitos com muitos pontos fora de controle que indicam um sistema de medição com baixa variação.

Gráfico Por peça
Este gráfico mostra as diferenças entre os níveis de fatores. Normalmente, os estudos de medição R&R organizam medições por peça e por operador. Entretanto, com o estudo de medição R&R expandido, é possível representar graficamente outros fatores.
No gráfico, os pontos representam as medições e símbolos de círculo-cruz representam as médias. A linha conecta as medições médias para cada nível de fator.
Observação
Se houver mais de 9 observações por nível, o Minitab exibe um boxplot em vez de um gráfico de valor individual.
Interpretação
Medições múltiplas para cada peça individual que variam o mínimo possível (os pontos para um lado estão juntos) indicam que o sistema de medição tem variação baixa. Além disso, as medições médias das peças deve variar o suficiente para demonstrar que as peças são diferentes e representam todo o intervalo do processo.
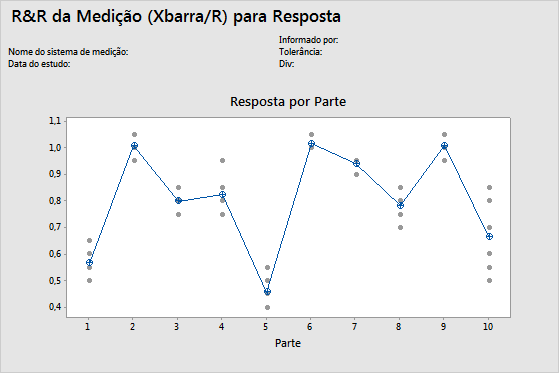
Gráfico Por Operador
O gráfico Por Operador exibe todas as medidas que foram tomadas no estudo, organizadas por operador. Este gráfico mostra as diferenças entre os níveis de fatores. Normalmente, os estudos de medição R&R organizam medições por peça e por operador. Entretanto, com o estudo de medição R&R expandido, é possível representar graficamente outros fatores.
Observação
Se houver menos de 10 observações por operador, o Minitab exibe um gráfico de valor individual em vez de um boxplot.
Interpretação
A linha horizontal que atravessa os operadores indica que as medições médias para cada operador são semelhantes. De maneira ideal, as medições para cada operador variam em igual quantidade.
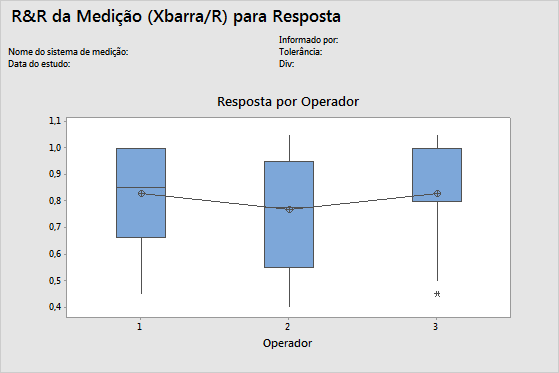
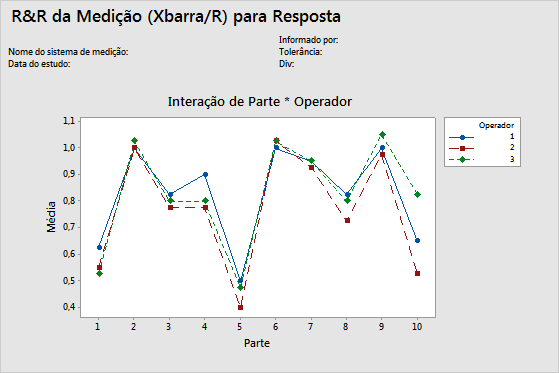
Gráfico de interação operador*peça
O gráfico de interação operador*peça mostra as medições médias de cada operador para cada peça. Cada linha conecta as médias de um único operador (ou de um termo que você especificar).
Os gráficos de interação apresentam a interação entre os dois fatores. Uma interação ocorre quando o efeito de um fator é dependente de um segundo fator. Este gráfico é o análogo gráfico da teste-f para um termo de interação na tabela ANOVA.
Interpretação
As linhas que são coincidentes indicam que os operadores medem de forma semelhante. Linhas que não são paralelas ou que se cruzam indicam que a capacidade de um operador medir uma peça consistentemente depende de qual peça está sendo medida. Uma linha que esteja constantemente mais alta ou mais baixa do que as outras indica que um operador adiciona vício à medição ao fazer consistentemente medições altas ou baixas.