Neste tópico
Vício
O vício é calculado como a diferença entre o valor padrão conhecido de uma peça de referência e a medição média observada.
- A estimativa do ponto de vício com um limite de tolerância inferior
- vício = limite inferior + interceptação / inclinação
- A estimativa do ponto de vício com um limite superior de tolerância
- vício = limite superior + interceptação / inclinação
A intercepção e a inclinação para ambas as fórmulas são da linha ajustada no gráfico de probabilidade.
O Minitab regride o score-z Φ-1(Prob (Aceitação)) nos valores de referência XT para calcular a interceptação e inclinação.
Repetibilidade pré-ajustada
A repetibilidade pré-ajustada é aquela que é calculada antes do ajuste para sobre-estimação.
Fórmula
O Minitab calcula a repetibilidade pré-ajustada por:

Notação
| Termo | Descrição |
|---|---|
| XT | representa os valores de referência estimados em probabilidades de aceitação de 0,995 e 0,005, que são calculados a partir da linha ajustada no gráfico de probabilidade. |
Repetibilidade
A repetibilidade é a quantidade de variação no sistema de medição que é do medidor. Um estudo de medição por atributos regride as probabilidades de aceitação sobre os valores de referência para obter repetibilidade.
A repetibilidade pré-ajustada é aquela que é calculada antes do ajuste para sobre-estimação. O Minitab divide as estimativas de repetibilidade pelo fator de ajuste de 1,08 para calcular a repetibilidade ajustada.
Fórmula
O Minitab estima a repetibilidade por:
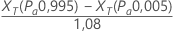
Notação
| Termo | Descrição |
|---|---|
| XT | representa os valores de referência estimados em probabilidades de aceitação de 0,995 e 0,005, que são calculados a partir da linha ajustada no gráfico de probabilidade. |
O denominador, 1,08 é o fator de ajuste dado pelo Automotive Industry Action Group (AIAG)1 O Minitab usa o valor de repetibilidade ajustado para testar vício = 0.
T para o método AIAG
Fórmula
Para testar vício = 0 utilizando o método de regressão, o Minitab usa a seguinte fórmula:
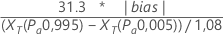
Notação
| Termo | Descrição |
|---|---|
| XT | representa os valores de referência estimados em probabilidades de aceitação de 0,995 e 0,005, que são calculados a partir da linha ajustada no gráfico de probabilidade. |
- 6 partes que têm aceitações maiores do que 0 e menos do que 20
- 1 peça tem 0 aceitações
- 1 peça tem 20 aceitações
T para o método de regressão
Fórmula
Para testar vício = 0 utilizando o método de regressão, o Minitab usa a seguinte fórmula:
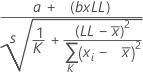
Notação
| Termo | Descrição |
|---|---|
| a | a intercepção da linha ajustada do gráfico de probabilidade |
| b | a inclinação da linha ajustada do gráfico de probabilidade |
| LL | limite inferior de tolerância |
| s | o desvio padrão do erro calculado utilizando a linha ajustada |
| K | o número de peças |
| xi | o valor de referência de cada peça |
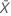 | a média dos valores de referência |
DF para o método AIAG
Os graus de liberdade são usados para calcular o valor de p.
DF = N – 1.
Notação
| Termo | Descrição |
|---|---|
| N | número de ensaios |
DF para o método de regressão
Os graus de liberdade são usados para calcular o valor de p.
DF = N – 2.
Notação
| Termo | Descrição |
|---|---|
| N | número de pontos utilizados para obter a linha ajustada |
valor de p
Os valores de p são usados em testes de hipóteses para ajudá-lo a decidir se deve rejeitar ou não rejeitar uma hipótese nula.
Para determinar se vício no sistema de medição é estatisticamente significativo, compare o valor-p com o nível de significância (denotado como α ou alfa). Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de concluir que existe vício quando não há nenhum vício significativo.
Linha ajustada
A linha ajustada é uma linha de regressão que examina a relação entre a probabilidade de aceitação e os valores de referência das peças medidas.
A forma geral de uma linha ajustada é: Y = b0 + b1 X
O Minitab regride o score-z Φ-1(Prob (Aceitação)) nos valores de referência XT para obter a interceptação e inclinação.
Notação
| Termo | Descrição |
|---|---|
| b0 | a interceptação — a constante que determina o posicionamento vertical da linha de regressão |
| b1 | a inclinação da linha de regressão |
| X | o valor da preditora |
R-sq para a linha ajustada
R-sq para a linha ajustada é o coeficiente de determinação, que é usado para verificar se a linha ajustada modela bem os dados. O valor de R-sq (R2) para a linha de regressão ajustada indica a porcentagem da variação na probabilidade de respostas de aceitação que é explicada pelo modelo de regressão.
R2 = 1 - (erro de SS / total de SS)
Notação
| Termo | Descrição |
|---|---|
| Erro de SS | soma do quadrado para o erro |
| SS total | soma dos quadrados total |
