Neste tópico
Vício
O vício é uma medida da precisão de um sistema de medição. O vício é calculado como a diferença entre o valor padrão conhecido de uma peça de referência e a medição média observada.
Interpretação
- Um vício positivo indica que o medidor mede alto.
- Um vício negativo indica que o medidor mede baixo.
Para um medidor que mede com precisão, o %bias será pequeno. Para determinar se o vício é estatisticamente significativo, use o valor de p.
Repetibilidade e repetibilidade pré-ajustada
A repetibilidade é a quantidade de variação no sistema de medição proveniente do medidor. Um estudo de medição de atributo regride as probabilidades de aceitação nos valores de referência para obter repetibilidade.
A repetibilidade pré-ajustada é aquela que é calculada antes do ajuste para sobre-estimação. O Minitab divide as estimativas de repetibilidade pelo fator de ajuste de 1,08 para calcular a repetibilidade ajustada. O fator de ajuste de 1,08 é dado pelo Automotive Industry Action Group (AIAG)1.
Interpretação
Um valor de repetibilidade baixo indica que o medidor mede de forma consistente. Um valor de repetibilidade alto indica variação aleatória, ou problemas, como uma seleção inadequada de peças ou medição insatisfatória.
O Minitab usa o valor de repetibilidade ajustado no cálculo para testar a hipótese nula de vício = 0.
Gráfico de probabilidade normal
O gráfico de probabilidade normal mostra a porcentagem de aceitações para cada valor de referência. Como não há medições reais do medidor disponíveis para estimar o vício e a repetibilidade, o Minitab calcula o vício e a repetibilidade ajustando a curva de distribuição normal usando as probabilidades de aceitação calculadas e os valores de referência conhecidos para todas as peças.
Se os erros de medição seguem uma distribuição normal, as probabilidades calculadas caem ao longo de uma linha reta. A linha de regressão se ajusta às probabilidades.
Interpretação
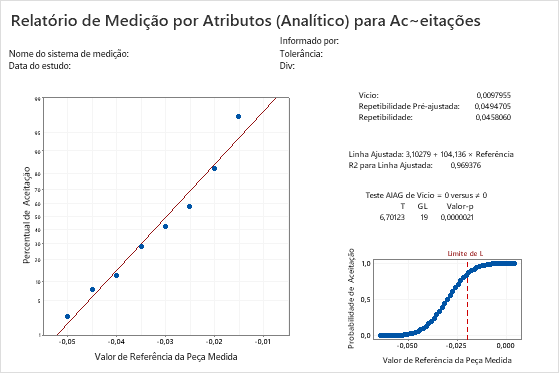
Linha ajustada
A probabilidade de aceitação de cada peça é calculada e plotada em um gráfico de probabilidade normal. Em um gráfico de probabilidade normal, o valor de y de um ponto plotado = Φ–1(Probabilidade de Aceitação), em que Φ–1 é o inverso da função de distribuição cumulativa normal padrão.
Uma linha de regressão ajustada é traçada através dos pontos plotados.
Interpretação
Se a linha ajustada for um bom ajuste para os pontos plotados, o Minitab usa os valores de interceptação e de declive para calcular os valores de vício e repetibilidade.

Este gráfico mostra que a linha ajustada se ajusta bem os dados.
R-sq para a linha ajustada
O valor de R-sq (R2) para a linha de regressão ajustada indica a porcentagem da variação na probabilidade de respostas de aceitação que é explicada pelo modelo de regressão.
Interpretação
R2 varia de 0 a 100%. Normalmente, quanto mais alto o valor de R2 melhor o modelo se ajusta aos seus dados. Os valores de R2 que são maiores do que 90% normalmente indicam um ajuste muito bom dos dados.

Para este exemplo, R-sq é 0,969376. A linha ajustada se ajusta aos dados muito bem, e o modelo é responsável por quase 97% da variância.
T
T é a estatística t para a hipótese alternativa que vício ≠ 0.
O teste t compara isso observando a estatística t para um valor crítico sobre a distribuição t com (n-1) graus de liberdade para determinar se o vício no sistema de medição é estatisticamente significativo.
DF
O valor de graus de liberdade (DF) é utilizado para determinar o valor de p. Para o método AIAG, DF = o número de ensaios -1. Para o método de regressão, DF é o número de pontos utilizados para criar a linha -2 ajustada.
Valor de p
Para determinar se vício no sistema de medição é estatisticamente significativo, compare o valor-p com o nível de significância (denotado como α ou alfa). Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de concluir que existe vício quando não há nenhum vício significativo.
Interpretação
Um valor de p menor fornece uma evidência mais forte contra a hipótese nula. Se o valor de p for menor que o valor de α, é possível rejeitar a hipótese nula de que o vício no sistema de medição é igual a 0.
Curva de desempenho de medição
A curva de desempenho de medição mostra a probabilidade estimada de aceitação como uma função do valor de referência para o produto. A linha de referência vertical indica o(s) limite(s) inserido(s) para a análise.
Interpretação
Se você especificar um limite de tolerância inferior, os valores de referência e probabilidades de aceitação mostram uma tendência crescente. Se você especificar um limite de tolerância superior, como o aumento de valores de referência, as probabilidades de aceitação diminuem.
Se um medidor tiver um limite superior e inferior e for possível assumir a linearidade e uniformidade de erro, você pode mostrar os dois limites de tolerância, superior e inferior, na curva de desempenho do medidor. A curva aparece como uma imagem espelhada.
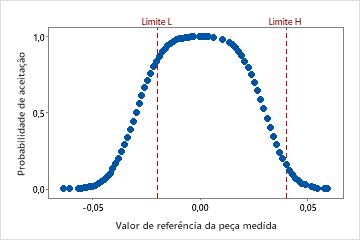
Por esses dados, a probabilidade de aceitação de um item no limite de tolerância inferior (Limite L) de -0,020 é alta. A probabilidade de aceitação aumenta à medida que os valores de referência aumentam até ao valor de referência de 0,01. Então a probabilidade de aceitação declina. A probabilidade de aceitação no limite de tolerância superior (Limite H) é de aproximadamente 0,15 de probabilidade.
