Neste tópico
Coeficiente de concordância de Kendall
Use a estatística de Kendall com dados ordinais de três ou mais níveis.
Na descrição do método, sem perda de generalidade, assumimos que é feita uma classificação única em cada indivíduo por cada avaliador, e existem k avaliadores por indivíduo. Então, para calcular o coeficiente de Kendall, os k avaliadores representam os k ensaios para cada avaliador.
Suponha que os dados estejam organizados em uma tabela k x N com cada linha representando as fileiras atribuídas por um avaliador específico aos indivíduos N.
Fórmulas
Quando o verdadeiro padrão não é conhecido, o Minitab calcula o coeficiente de Kendall por:
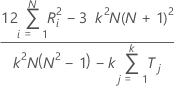
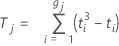
Notação
| Termo | Descrição |
|---|---|
| N | o número de indivíduos |
| Σ Ri2 | a soma dos quadrados dos totalizados das classificações para cada um dos N indivíduos classificados |
| K | o número de avaliadores |
| Tj | Tj atribui a média das classificações à observação empatada |
| Termo | Descrição |
|---|---|
| ti | o número de classificações empatadas no io agrupamento de empates |
| gj | o número de grupos de empates no jo conjunto de classificações |
Testando a significância do coeficiente de Kendall da concordância
Para testar a significância do coeficiente de Kendall, use:
c 2= k (N – 1) W
Notação
| Termo | Descrição |
|---|---|
| c 2 | é distribuída como qui-quadrado com N - 1 graus de liberdade |
| k | o número de avaliadores |
| N | o número de indivíduos |
| W | coeficiente de Kendall calculado |
Coeficiente de correlação de Kendall
Use a estatística de Kendall com dados ordinais de três ou mais níveis.
Na descrição do método, sem perda de generalidade, podemos supor que uma classificação única em cada sujeito é feita por cada avaliador, e existem k avaliadores por sujeito. Então, para calcular o coeficiente de correlação de Kendall, os k avaliadores representam os k ensaios feitos por todos os avaliadores.
Quando o verdadeiro padrão é conhecido, o Minitab calcula o coeficiente de correlação de Kendall, calculando a média de coeficientes de Kendall entre cada avaliador e o padrão.
Coeficiente de correlação de Kendall para a concordância dos testes com o padrão conhecido é a média dos coeficientes de correlação de Kendall entre os ensaios.
Fórmulas
O Minitab calcula o coeficiente de Kendall entre cada ensaio e o padrão usando:

Notação
| Termo | Descrição |
|---|---|
| TX | número de pares empatados em X = 0,5 Σi ni+ (ni+– 1) |
| TY | número de pares empatados em Y = 0,5 Σj n+j (n+j– 1) |
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares discordantes = Σi<kΣj>l nij nkl |
| Termo | Descrição |
|---|---|
| ni+ | número de observações na ia linha |
| n+j | número de observações na ja coluna |
| nij | observações na célula correspondente à ia linha e ja coluna |
| nkl | observações na célula correspondente à ka linha la coluna |
| n++ | número de observações total |
Referência
A. Agresti (1984). Analysis of Ordinal Categorical Data, John Wiley & Sons.
Testando a significância do coeficiente de correlação de Kendall
Fórmula
Para testar a significância do coeficiente de Kendall quando o verdadeiro padrão é conhecido, use:
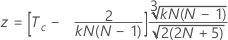
use:
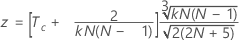
Notação
| Termo | Descrição |
|---|---|
| Tc | a média dos coeficientes de correlação de Kendall entre cada avaliador e o padrão |
| N | o número total de indivíduos |
| k | o número total de classificadores |
