Métodos e fórmulas para estatísticas kappa para Análise de concordância por atributos

Selecione o método ou a fórmula de sua escolha.

Neste tópico

estatísticas kappa de Cohen (padrão desconhecido)
Estatísticas kappa de Cohen (padrão conhecido)
Teste de significância de kappa de Cohen
Estatística kappa de Fleiss (padrão desconhecido)
Testes de significância de kappa de Fleiss (padrão desconhecido)
Estatística kappa de Fleiss (padrão conhecido)
Testar a significância de kappa de Fleiss (padrão conhecido)

estatísticas kappa de Cohen (padrão desconhecido)

Use a estatística kappa de Cohen quando as classificações forem nominais. Quando o padrão não for conhecido e você optar por obter kappa de Cohen, o Minitab irá calcular a estatística quando os dados atenderem às seguintes condições:

Dentro do avaliador — há exatamente dois ensaios com um avaliador
Entre avaliadores — há exatamente dois avaliadores, cada um com apenas um ensaio

Para um valor resposta específico, kappa pode ser calculado pelo colapso que todas as respostas que não são iguais ao valor em uma categoria. Então, você pode usar a tabela de 2X2 para calcular kappa.

Fórmulas

Quando o padrão verdadeiro é desconhecido, o Minitab estima kappa de Cohen por:

	Ensaio B (ou Avaliador B)
Ensaio A (ou Avaliador A)	1	2	...	k	Total
1	p₁₁	p₁₂	...	p_1k	p₁₊
2	p₂₁	p₂₂	...	p_2k	P₂₊
....
k	p_k1	p_k2	...	p_kk	p_k+.
Total	p_.+1	p_.+2	...	p_.+k	1

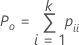
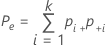
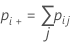
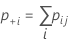
Notação

Termo	Descrição
P_o	a proporção observada da concordância
p_ii	cada valor na diagonal da tabela de duas vias
P_e	a proporção esperada de k vezes que os avaliadores concordam
n_ij	o número de amostras na i^a linha e na j^a coluna
N	o número total de amostras

Estatísticas kappa de Cohen (padrão conhecido)

Use a estatística kappa de Cohen quando as classificações forem nominais. Quando o padrão for conhecido e você optar por obter kappa de Cohen, o Minitab irá calcular a estatística usando as fórmulas abaixo:

O coeficiente de kappa para a concordância de ensaios com o padrão conhecido é a média desses coeficientes de kappa.

Fórmulas

Quando o padrão verdadeiro é conhecido, em primeiro lugar, calcule kappa usando os dados de cada ensaio e o padrão conhecido.

	Padrão
Ensaio A	1	2	...	k	Total
1	p₁₁	p₁₂	...	p_1k	p₁₊
2	p₂₁	p₂₂	...	p_2k	P₂₊
....
k	p_k1	p_k2	...	p_kk	p_k+.
Total	p_.+1	p_.+2	...	p_.+k	1

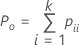
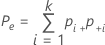
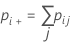
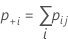
Notação

Termo	Descrição
P_o	a proporção observada da concordância
p_ii	cada valor na diagonal da tabela de duas vias
P_e	a proporção esperada de k vezes que os avaliadores concordam
n_ij	o número de amostras na i^a linha e na j^a coluna
N	o número total de amostras

Teste de significância de kappa de Cohen

Para testar a hipótese nula de que as classificações são independentes (de modo que kappa = 0), use:

z = kappa / SE de kappa

Este é um teste unilateral. Sob a hipótese nula, z segue a distribuição normal padrão. Rejeite a hipótese se z for significativamente maior do que o valor crítico α.

Fórmulas

O erro padrão da kappa para cada ensaio e o padrão é:

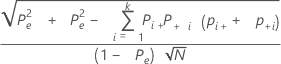
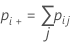
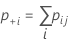
Notação

Termo	Descrição
P_e	a proporção esperada de k vezes que os avaliadores concordam
N	o número total de amostras

Estatística kappa de Fleiss (padrão desconhecido)

Há dois casos de cálculo da estatística kappa.

Caso 1 — Concordância dentro de cada avaliador: Calcular os coeficientes de kappa que representam a concordância dentro de cada avaliador.; Neste caso, m = número de ensaios dentro de cada avaliador, assume-se que m seja > 1. O analista está interessado em examinar a concordância entre os ensaios m dentro de cada avaliador. Aqui assumimos que cada tentativa é feita sob a condição de que o avaliador não se lembra as classificações dos ensaios anteriores.
Caso 2 — Concordância entre todos os avaliadores: Calcular os coeficientes de kappa que representam a concordância entre todos os avaliadores.; Neste caso, m = ao número total de ensaios em todos os avaliadores. Supõe-se que o número de avaliadores seja > 1, o número de ensaios pode ser 1 ou > 1. O analista está interessado na concordância de todos os avaliadores.

Fórmulas para o kappa global

Definir x_ij como o número de classificações no exemplo i na categoria j, em que i é desde 1 até n, e j é de 1 a k.

O coeficiente kappa global é definido por:

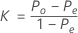
em que:

P_o é a proporção observada da concordância para pares entre m ensaios.

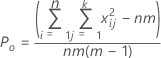
P_e é a proporção esperada de concordância se as classificações de um ensaio for independente do outro.

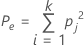
p_j representa a proporção global de classificações na categoria j.

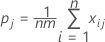
Substituindo P_o e P_e por K, o coeficiente de kappa total é estimado por:

onde:

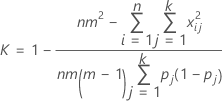
Termo	Descrição
k	o número de categorias total
m	o número de ensaios — para o caso 1, m = número de ensaios para cada avaliador; para o caso 2, m = número de ensaios para todos os avaliadores.
n	o número de amostras.
x_ij	o número de classificações na amostra i na categoria j

Fórmulas para kappa para uma única categoria

Para a medição da concordância no que se refere às classificações em uma única das k categorias, digamos a j^a, é possível combinar todas as categorias, exceto aquela de interesse atual, em uma única categoria e aplicar a equação acima. A fórmula resultante da estatística kappa para a j^a categoria é:

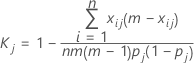
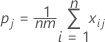
onde:

Termo	Descrição
k	o número de categorias total
m	o número de ensaios — para o caso 1, m = número de ensaios para cada avaliador; para o caso 2, m = número de ensaios para todos os avaliadores.
n	o número de amostras.
x_ij	o número de classificações na amostra i na categoria j

Testes de significância de kappa de Fleiss (padrão desconhecido)

A hipótese nula, H₀, é kappa = 0. A hipótese alternativa, H₁, é kappa > 0.

Sob a hipótese nula, Z é uma aproximadamente normalmente distribuído e é usado para calcular os valores de p.

Fórmulas

Para testar se kappa> 0, use a seguinte estatística de Z:

Var (K) é calculado por:

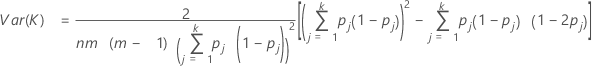
Para testar se kappa > 0 para a j^a categoria, use a estatística de Z a seguir:

Var (K_j) é calculada por:

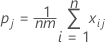
Notação

Termo	Descrição
K	a estatística Kappa global
K_j	a estatística de kappa para a j^a categoria
k	o número de categorias total
m	o número de ensaios — para o caso 1, m = número de ensaios para cada avaliador; para o caso 2, m = número de ensaios para todos os avaliadores.
n	o número de amostras.
x_ij	o número de classificações na amostra i na categoria j

Estatística kappa de Fleiss (padrão conhecido)

Use as etapas a seguir para calcular kappa e kappa global para uma categoria específica quando a classificação padrão para cada amostra é conhecida.

Suponha que existam m ensaios.

Observação

Veja as fórmulas da estatística kappa de Fleiss (padrão desconhecido).

Para cada ensaio, calcule kappa utilizando as classificações do ensaio, e as classificações dadas pelo padrão. Em outras palavras, trate o padrão como outro ensaio, e use as fórmulas desconhecidas de kappa padrão para dois ensaios para estimar kappa.
Repita o cálculo para todos os m ensaios.
Agora você tem m valores de kappa globais e m valores de kappa para os valores de categoria específicos.

O kappa global com padrão conhecido é, então, igual à média de todos os valores de kappa globais de m.

Da mesma forma, o kappa para uma categoria específica com padrão conhecido é a média de todos os m kappa para valores de categoria específicos.

Testar a significância de kappa de Fleiss (padrão conhecido)

A hipótese nula, H₀, é kappa = 0. A hipótese alternativa, H₁, é kappa > 0.

Sob a hipótese nula, Z é uma aproximadamente normalmente distribuído e é usado para calcular os valores de p.

Onde K é a estatística kappa, Var (K) é a variância da estatística kappa.

Observação

Veja as fórmulas da estatística kappa de Fleiss (padrão desconhecido)

Suponha que existam m ensaios.

Para cada ensaio, calcule a variância de kappa utilizando as classificações do ensaio, e as classificações dadas pelo padrão. Em outras palavras, trate o padrão como o segundo ensaio, e use a variância das fórmulas de kappa para os dois ensaios e para o caso padrão desconhecido a fim de calcular a variância.
Repita o cálculo para todos os m ensaios
Agora você tem m variâncias para kappa geral e m variâncias para kappa para categorias específicas.

A variância de kappa geral com padrões conhecidos é, nesse caso, igual à soma das m variâncias para kappa geral dividida por m².

Da mesma forma, a variância de kappa para uma categoria específica com padrão conhecido é igual à soma das variâncias de m para kappa para uma categoria específica dividida por m².