Se seus dados apresentam sobredispersão ou subdispersão, uma carta de atributos de Laney (uma Carta P de Laney ou uma Carta U de Laney) pode distinguir entre a variação de causa comum e a variação de causa especial com mais exatidão do que uma carta de atributos tradicional (por exemplo, umaCarta P ou uma Carta U). Os cálculos das cartas de atributos de Laney incluem Sigma Z, que é um ajuste para sobredispersão ou subdispersão. Um valor Sigma Z de 1 indica que nenhum ajuste é necessário e que a carta e atributos de Laney é exatamente o mesmo que uma carta de atributos tradicional.
Para criar uma carta P' de Laney, selecione . Para criar uma carta U' de Laney, selecione .
O que é superdispersão?
A superdispersão existe quando os dados exibem mais variação do que você esperaria com base em uma distribuição binomial (para unidades defeituosas) ou uma distribuição de Poisson (para defeitos). Cartas P e cartas U tradicionais assumem que sua taxa de unidades defeituosas ou defeitos permanece constante ao longo do tempo. Contudo, fatores de ruídos externos, que não são causas especiais, normalmente causam alguma variação na taxa de unidades defeituosas ou defeitos ao longo do tempo.
Os limites de controle em uma carta P ou carta U tradicional ficam mais estreitos quando seus subgrupos são maiores. Se seus subgrupos forem grandes o suficiente, a sobredispersão pode fazer com que pontos pareçam estar fora de controle quando eles não estão. Para uma carta de atributos de Laney, a definição de variação de causa comum inclui não apenas a variação dentro do subgrupo, mas também a variação média entre subgrupos consecutivos. Se houver sobredispersão, os limites de controle na carta de atributos de Laney são mais amplos do que aqueles de uma carta de atributos tradicional.
A relação entre o tamanho do subgrupo e os limites de controle em uma carta de controle de atributos tradicional é similar àquela entre o poder e um teste t para 1 amostras. Com amostras maiores, o teste t tem mais poder para detectar uma diferença. Contudo, se a amostra for grande o suficiente, até mesmo uma diferença muito pequena que não é interessante, pode se tornar significativa. Por exemplo, com uma amostra de 1.000.000 de observações, um teste t pode determinar que uma média amostral de 50.001 é significativamente diferente de 50. Contudo, uma diferença de 0,001 pode não ter implicações práticas para o seu processo.
O que é subdispersão?
A subdispersão é o oposto da superdispersão. A subdispersão existe quando os dados exibem menos variação do que você esperaria com base em uma distribuição binomial (para unidades defeituosas) ou uma distribuição de Poisson (para defeitos). A subdispersão pode ocorrer quando subgrupos adjacentes estão correlacionados uns com os outros, o que também é conhecido como autocorrelação.
Quando os dados apresentam subdispersão, os limites de controle em uma carta P ou carta U tradicional pode ser muito largos. Se os limites de controle forem muito amplos, você pode ignorar a variação de causa especial e confundi-la com a variação de causa comum. Se houver subdispersão, os limites de controle em um gráfico de atributos de Laney são mais estreitos do que os de uma carta de atributos tradicional.
Por exemplo, conforme uma ferramenta se desgasta, o número de defeitos pode aumentar. O aumento na contagem de defeitos entre os subgrupos pode tornar os subgrupos mais semelhantes do que seria por acaso.
Comparação de cartas de atributos tradicionais com cartas de atributos do Laney
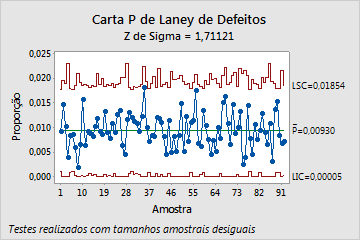
Os gráficos a seguir mostram uma carta P tradicional e uma carta P' de Laney referentes aos mesmos dados. Esses dados também são apresentados no exemplo da carta P' de Laney e no exemplo do Diagnóstico de Carta P. Os subgrupos são muito grandes, com uma média de aproximadamente 2500 observações em cada um. Além disso, o teste de Diagnóstico de Carta P revela sobredispersão nos dados.
Os tamanhos de subgrupos grandes resultam em limites de controle muito estreitos na carta P tradicional. Com os limites de controle estreitos, a sobredispersão faz com que vários subgrupos pareçam fora de controle. A carta P' de Laney, no entanto, corrige a sobredispersão e mostra que o processo está realmente sob controle. Nenhum ponto está fora dos limites de controle.
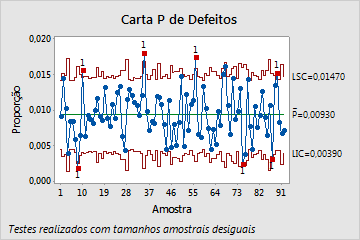
Carta P tradicional