O desvio padrão do processo também é chamado de sigma ou σ. Se você inserir um valor histórico para sigma, o Minitab usa o valor histórico. Caso contrário, o Minitab utiliza um dos métodos a seguir para estimar sigma a partir dos dados.
Neste tópico
Método Rbar
O Minitab usa o intervalo de cada subgrupo, 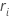 , para calcular
, para calcular 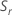 , que é um estimador não viciado de σ:
, que é um estimador não viciado de σ:
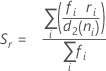
onde
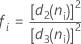
Quando o tamanho do subgrupo é constante, a fórmula simplifica para o seguinte:
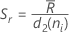
onde 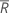 (Rbar) é a média dos intervalos do subgrupo, calculada da seguinte maneira:
(Rbar) é a média dos intervalos do subgrupo, calculada da seguinte maneira:

Notação
| Termo | Descrição |
|---|---|
| ri | intervalo para o subgrupo i |
| m | número de subgrupos |
| d2(·) | valor da constante não-viciada d2 que corresponde ao valor especificado entre parênteses. |
| ni | número de observações no subgrupo i |
| d3(·) | valor da constante não-viciada d3 que corresponde ao valor especificado entre parênteses. |
Método Sbar
Sem constante não-viciada c4'()
Se você não usar uma constante não-viciada, o Sbar é a média dos desvios padrão do subgrupo:
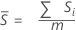
Com a constante não-viciada
Se você usar a constante não-viciada, c4(ni), Sbar é calculada da seguinte maneira:
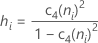
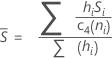
Quando o tamanho do subgrupo for constante, Sbar é:
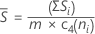
Notação
| Termo | Descrição |
|---|---|
| c4 (ni) | valor da constante não-viciada c4 que corresponde ao valor que é especificado entre parênteses. |
| Si | desvio padrão do subgrupo i |
| m | número de subgrupos |
Método do desvio padrão combinado
O desvio padrão combinado (Sp) é dado pela seguinte fórmula:
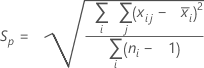
Quando o tamanho do subgrupo é constante, Sp também pode ser calculado da seguinte maneira:

Com a constante não-viciada
Por padrão, o Minitab aplica a constante não-viciada, c4(), quando você usa o desvio padrão combinado para estimar σ:
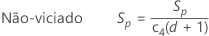
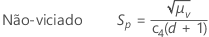
Notação
| Termo | Descrição |
|---|---|
| xij | ja observação no io subgrupo |
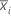 | média do subgrupo i |
| ni | número de observações no subgrupo i |
| μv | média das variâncias do subgrupo |
| c4(·) | valor da constante não-viciada c4 que corresponde ao valor que é especificado entre parênteses. |
| d | os graus de liberdade para Sp, dados pela seguinte fórmula:
 |
Constantes não-viciadas 2(), d3() e d4()
d2(N) é o valor esperado do intervalo de N observações a partir de uma população normal, com desvio padrão = 1. Assim, se r é o intervalo de uma amostra de N observações de uma distribuição normal com desvio padrão = σ, E(r) = d2(N)σ.
d3(N) é o desvio padrão do intervalo de N observações de uma população normal com σ = 1. Assim, se r for o intervalo de uma amostra de N observações a partir de uma distribuição normal com desvio padrão = σ, stdev(r) = d3(N)σ.
Use a tabela a seguir para encontrar uma constante não-viciada para um dado valor, N. (Para determinar o valor de N, consulte a fórmula para a estatística de interesse).

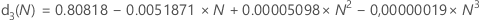
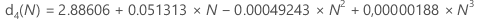
- D. J. Wheeler and D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
- H. Leon Harter (1960). "Tables of Range and Studentized Range". The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1,128 | 0,8525 | 0,954 |
| 3 | 1,693 | 0,8884 | 1,588 |
| 4 | 2,059 | 0,8798 | 1,978 |
| 5 | 2,326 | 0,8641 | 2,257 |
| 6 | 2,534 | 0,848 | 2,472 |
| 7 | 2,704 | 0,8332 | 2,645 |
| 8 | 2,847 | 0,8198 | 2,791 |
| 9 | 2,97 | 0,8078 | 2,915 |
| 10 | 3,078 | 0,7971 | 3,024 |
| 11 | 3,173 | 0,7873 | 3,121 |
| 12 | 3,258 | 0,7785 | 3,207 |
| 13 | 3,336 | 0,7704 | 3,285 |
| 14 | 3,407 | 0,763 | 3,356 |
| 15 | 3,472 | 0,7562 | 3,422 |
| 16 | 3,532 | 0,7499 | 3,482 |
| 17 | 3,588 | 0,7441 | 3,538 |
| 18 | 3,64 | 0,7386 | 3,591 |
| 19 | 3,689 | 0,7335 | 3,64 |
| 20 | 3,735 | 0,7287 | 3,686 |
| 21 | 3,778 | 0,7242 | 3,73 |
| 22 | 3,819 | 0,7199 | 3,771 |
| 23 | 3,858 | 0,7159 | 3,811 |
| 24 | 3,895 | 0,7121 | 3,847 |
| 25 | 3,931 | 0,7084 | 3,883 |
| N | d2(N) |
|---|---|
| 26 | 3,964 |
| 27 | 3,997 |
| 28 | 4,027 |
| 29 | 4,057 |
| 30 | 4,086 |
| 31 | 4,113 |
| 32 | 4,139 |
| 33 | 4,165 |
| 34 | 4,189 |
| 35 | 4,213 |
| 36 | 4,236 |
| 37 | 4,259 |
| 38 | 4,28 |
| 39 | 4,301 |
| 40 | 4,322 |
| 41 | 4,341 |
| 42 | 4,361 |
| 43 | 4,379 |
| 44 | 4,398 |
| 45 | 4,415 |
| 46 | 4,433 |
| 47 | 4,45 |
| 48 | 4,466 |
| 49 | 4,482 |
| 50 | 4,498 |
Constantes não viciadas c4() e c5()
c4()

c5()

Notação
| Termo | Descrição |
|---|---|
| Γ() | função gama |
