Selecione o método ou a fórmula de sua escolha.
Plano CUSUM, h, k e FIR
Com processos sob controle, as cartas CUSUM são boas para detectar pequenas mudanças de distância do alvo, porque elas incorporam informações da sequência de valores de amostra. Os pontos representados graficamente são as somas acumuladas dos desvios dos valores de amostra do alvo. Estes pontos devem variar aleatoriamente em torno de zero. Se a tendência se desenvolve para cima ou para baixo, deve-se considerar como prova de que a média do processo mudou, e você deve olhar para as causas especiais.
- CUSUM tabular (o padrão)
- A CUSUM superior detecta mudanças para cima no nível do processo e a CUSUM inferior detecta mudanças em baixa. Esta carta usa limites de controle (UCL e LCL) para determinar quando uma situação fora de controle ocorreu. Consulte Prins et al.1 and Stoumbos et al.2 para obter detalhes sobre uma discussão de CUSUMs tabulares.
- CUSUM com máscara V
- Esta carta usa uma máscara V em vez de limites de controle para determinar quando uma situação fora de controle ocorreu. Consulte Lucas3 and Wadsworth et al.4 para visualizar uma discussão sobre a carta de máscara V.
As cartas CUSUM são definidas por dois parâmetros, h e k, que são também muito conhecixas como plano CUSUM. Estes valores são, por vezes, selecionados de tabelas ARL (Duração Média do Ensaio). Consulte Lucas3 e Lucas et al.5.
h
Para CUSUMs tabulares, h é o número de desvios padrão entre a linha central e os limites de controle. É o valor em que ocorre um sinal fora de controle.
Para CUSUMs de máscara V, o Minitab calcula a metade da largura da máscara V (H) no ponto de originação por H = hσ.
O valor padrão por h é 4.
k
Para CUSUMs tabulares, k é a "folga" admissível no processo. Na fórmula do ponto CUSUM, k especifica o tamanho da mudança que você deseja detectar.
Para CUSUMs de máscara V, k é a inclinação dos braços da máscara V. Para CUSUMs de máscara V, k é a inclinação dos braços da máscara V.
O valor padrão por h é 0,5.
FIR
FIR (resposta inicial rápida) é um método usado para inicializar a CUSUM tabular. Normalmente, as CUSUMs tabulares são inicializadas em 0, mas se o processo estiver fora de controle na inicialização, as CUSUMs não irão detectar a situação para os vários subgrupos.CUSUM tabular
Pontos representados graficamente
Os dados representados graficamente em uma carta CUSUM são CLi, CUi.
O valor de uma carta CUSUM tabular inferior no momento i:

em que:

O valor de uma carta CUSUM tabular superior no momento i:

em que:
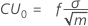
Linha central
Para o padrão, a carta CUSUM tabular, a linha central é 0.
Limite de controle inferior (LCL)
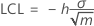
Limite de controle superior (UCL)
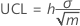
Notação
| Termo | Descrição |
|---|---|
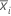 | média de subgrupo |
| T | alvo |
| k | tamanho da mudança que você deseja detectar |
| σ | desvio padrão do processo |
| m | tamanho do subgrupo |
| f | FIR |
| h | intervalo de decisão |
CUSUM com máscara V
Pontos representados graficamente
Ci, o valor de uma carta CUSUM com máscara V no momento i =
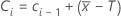
onde C0 = 0
inclinação da máscara V

largura da máscara V na origem
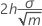
origem da máscara V
A carta padrão usa n para estimar o p de origem.
Notação
| Termo | Descrição |
|---|---|
| T | alvo |
| k | inclinação do braço da máscara V |
| h | intervalo de decisão |
| m | tamanho do subgrupo |
Métodos e fórmulas para Box-Cox
Fórmula Box-Cox
Se você usar a transformação de Box-Cox, o Minitab transformará os valores de dados originais (Yi), de acordo com a seguinte fórmula:
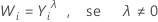
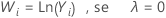
onde λ é o parâmetro para a transformação. O Minitab então, cria uma carta de controle dos valores de dados transformados (Wi). Para aprender como o Minitab seleciona o valor ótimo de λ, acesse Métodos e fórmulas para Transformação de Box-Cox.
Valores de λ comuns
| λ | Transformação |
|---|---|
| 2 | 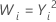 |
| 0,5 |  |
| 0 |  |
| −0,5 | 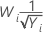 |
| −1 | 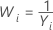 |
