Selecione o método ou a fórmula de sua escolha.
Neste tópico
Pontos representados graficamente
Dados em subgrupos
Quando os dados estão em subgrupos, T2 é calculado da seguinte forma:
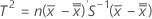
onde:
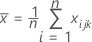
 é o vetor médio de
é o vetor médio de 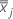 (média dos valores de xjk ), que é calculada da seguinte forma:
(média dos valores de xjk ), que é calculada da seguinte forma:
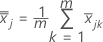
S = matriz de covariância da amostra
A matriz de covariância da amostra, S, é calculada da seguinte maneira:

onde:
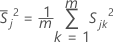
onde:
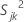 , a variância amostral para a j-ésima característica na k-ésima amostra, é calculada da seguinte forma:
, a variância amostral para a j-ésima característica na k-ésima amostra, é calculada da seguinte forma:
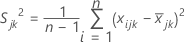
onde:
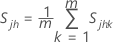
onde:
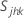 , a covariância, =
, a covariância, =
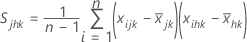
A média das matrizes S é de uma estimativa não-viciada da variância, quando o processo está sob controle. n deve ser maior do que p e não deve haver fortes correlações entre as variáveis de modo que a matriz de covariância de amostra não seja singular.
Quando os dados estão em subgrupos, o gráfico exibe um valor ausente para qualquer subgrupo que seja uma observação individual.
Observações individuais
Quando os dados são observações individuais, T2 é calculado da seguinte forma:
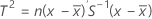
onde:
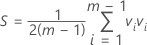
onde:

Notação
| Termo | Descrição |
|---|---|
| n | Tamanho amostral |
 | vetor da média da amostra |
| xijk | a i-ésima observação sobre a j-ésima característica na késima amostra |
| m | número amostras |
Exemplo de cálculo de T2
O Minitab representa graficamente a estatística T2 em uma carta de controle. Se um ponto representado graficamente estiver fora dos limites de controle, o processo está fora de controle naquele ponto. Veja as equações de tabela e de amostra para referência dos cálculos do Minitab.
Os dados a seguir são provenientes de um processo de desenvolvimento de solução de limpeza. As quantidades de citrato de sódio e glicerina afetam a potência da solução.
| Médias dos subgrupos | Variâncias e covariâncias | Estatística T2 | ||||
| Subgrupo | Citrato de sódio (X1) | Glicerina (X2) | S 1 2 | S2 2 | S 1 2 k | T2 |
| 1 | 125 | 025 | 7292 | 8692 | 5791 | 5708 |
| 2 | 625 | 4 | 2292 | 2333 | 3333 | 1429 |
| 3 | 4 | 875 | 1467 | 0625 | 8000 | 9528 |
| 4 | 2 | 2 | 2933 | 7600 | 6667 | 8073 |
| 5 | 25 | 225 | 2500 | 2692 | 7917 | 7548 |
| 6 | 4 | 45 | 6667 | 9567 | 3333 | 2711 |
| 7 | 275 | 025 | 3692 | 4692 | 7108 | 7785 |
| 8 | 6 | 65 | 4333 | 7700 | 6933 | 6183 |
| 9 | 625 | 325 | 7892 | 5558 | 1325 | 3592 |
| 10 | 3 | 5 | 2867 | 9467 | 2600 | 4942 |
| 11 | 25 | 5 | 1767 | 1200 | 9000 | 3279 |
| 12 | 1 | 625 | 1467 | 1692 | 4033 | 0277 |
| Médias | 7875 | 2333 | 7931 | 9318 | 3003 | |
- Calcular a média de subgrupo para cada variável, X1 e X2. Neste caso, cada subgrupo tinha quatro amostras.
- Se você tiver observações individuais, o Minitab as utiliza em vez das médias de subgrupo em todos os cálculos.
- Calcular as variâncias de subgrupo, S1 2 e S2 2.
- Calcular as covariâncias de subgrupo, S1 2 k.
- Calcular as médias da média de subgrupo, as médias das variâncias de subgrupo e a as médias das covariâncias.
- Designar a matriz de covariância da amostra S e o vetor médio.
- Calcular T2, que é dado por:
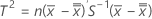
O Minitab representa graficamente T2 na carta T2 e compara-o com os limites de controle para determinar se os pontos individuais estão fora de controle.
Linha central
A linha central para a carta T2 é KX. O cálculo de K e X depende do tamanho máximo da amostra e se Minitab calcula a matriz de covariância dos dados.
Dados em subgrupos
Quando os dados estão em subgrupos, KX é calculado da seguinte maneira:
- Matriz de covariância dada
-


- Matriz de covariância estimada
-


Observações individuais
Quando os dados são observações individuais, KX é calculado da seguinte maneira:
- Matriz de covariância dada
-
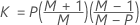
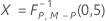
- Matriz de covariância estimada
-
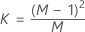
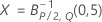
em que:
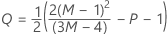
Notação
| Termo | Descrição |
|---|---|
| P | número de variáveis |
| M | número de subgrupos |
| N | tamanho amostral |
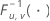 | a distribuição F acumulada inversa com u graus de liberdade do numerador e v graus de liberdade do denominador |
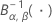 | a distribuição beta acumulada inversa com o primeiro parâmetro de forma α e o segundo parâmetro de forma β |
Limite de controle
Dados em subgrupos
O limite de controle superior, se você não especificar os parâmetros, é:
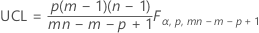
O limite de controle superior, se você especificar os parâmetros, é:
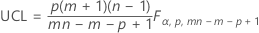
Observações individuais
O limite de controle superior, se você não especificar os parâmetros, é:
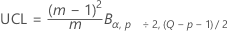
em que:
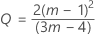
Consulte Woodall et al.1 para obter mais informações.
O limite de controle superior, se você especificar os parâmetros, é:
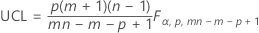
Notação
| Termo | Descrição |
|---|---|
| α | valor fixo de 0,00134989803156746 |
| p | número de características |
| m |
Para dados em subgrupos, se não forem especificadas as estimativas de parâmetros, m é o número de amostras. Se forem fornecidas as estimativas dos parâmetros, m é o número de amostras utilizadas para criar a matriz de covariâncias. Para dados individuais, m é o número de observações. |
| n | tamanho de cada amostra |
| F | indica que a distribuição F é usada |
| B | indica que a distribuição beta é usada |
Estatística T2 descomposta
Estatística T2 descomposta:
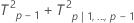
em que:

em que:
xi(p − 1)é o vetor médio decomposto
Sxx é a submatriz principal (p – 1) × (p – 1) de S
T2p|1,..., p−1 é uma aproximação diferente para as fases e se você tem subgrupos ou observações individuais:
Fase 1 para dados nos subgrupos
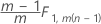
Fase 2 para dados nos subgrupos
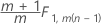
Fase 1 para observações individuais
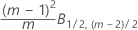
Fase 2 para observações individuais
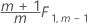
O Minitab calcula os limites de controle da fase 1 quando você não especificar as estimativas de parâmetros e os limites de controle da fase 2 quando você especificar.
Consulte Mason et al.2 para obter mais informações sobre a estatística T2 decomposta.
Notação
| Termo | Descrição |
|---|---|
| m | número de amostras |
| F | indica que a distribuição F é usada |
| B | indica que a distribuição beta é usada |
Métodos e fórmulas para Box-Cox
Fórmula Box-Cox
Se você usar a transformação de Box-Cox, o Minitab transformará os valores de dados originais (Yi), de acordo com a seguinte fórmula:
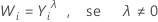
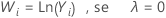
onde λ é o parâmetro para a transformação. O Minitab então, cria uma carta de controle dos valores de dados transformados (Wi). Para aprender como o Minitab seleciona o valor ótimo de λ, acesse Métodos e fórmulas para Transformação de Box-Cox.
Valores de λ comuns
| λ | Transformação |
|---|---|
| 2 | 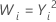 |
| 0,5 |  |
| 0 |  |
| −0,5 | 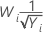 |
| −1 | 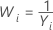 |
