Neste tópico
Pontos representados graficamente
Cada ponto na carta U' de Laney representa o número de defeitos por unidade de medição.
Interpretação
Se o processo estiver sob controle, os pontos variam aleatoriamente em torno da linha central, e o processo exibe apenas as variações de causa comum. Investigue os pontos que estão fora dos limites de controle ou que apresentam padrões não aleatórios quanto a uma possível variação de causa especial.
Linha central
A linha central na carta U' de laney representa o número médio de defeitos por unidade de medição. O número médio de defeitos por unidade também é chamado de média do processo.
Interpretação
Utilize a linha central para observar como é o desempenho do processo em relação à média. Se o processo estiver sob controle, os pontos variam aleatoriamente em torno da linha central.
Cautela
Não confunda a linha central com o valor alvo para o seu processo. O alvo é o resultado desejado. A linha central é o resultado real.
Limites de controle
Cautela
Não confunda limites de controle com limites de especificação. Limites de especificação representam os requisitos do cliente e indicam a quantidade de variação que você quer ver no processo. Os limites de controle representam a quantidade real de variação que está nos dados da amostra. Um processo pode estar sob controle, mas não ser capaz de atender especificações.
Sigma Z
Sigma Z mede sobre ou subdispersão em seus dados.
Interpretação
- Um valor de Sigma Z de 1 indica que nenhum ajuste é necessário. Neste caso, os limites de controle na carta U' de Laney são exatamente iguais aos limites de controle de uma carta U tradicional.
- O valor de Sigma Z maior do que 1 indica que os limites de controle na carta U' de Laney são mais amplos do que aqueles em uma carta U tradicional para o ajuste para sobredispersão.
- O valor de Sigma Z menor do que 1 indica que os limites de controle na carta U' de Laney são mais estreitos do que aqueles em uma carta U tradicional para o ajuste para subdispersão.
Por exemplo, os gráficos a seguir mostram uma carta P tradicional e uma carta U' de Laney dos mesmos dados. Os subgrupos são grandes e seus dados exibem sobredispersão.
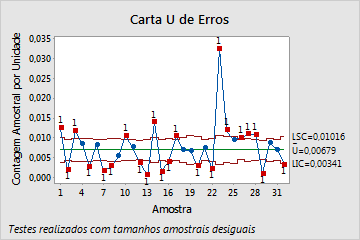
- Carta U tradicional
- Na carta U tradicional, os tamanhos de subgrupos grandes resultam em limites de controle estreitos. Os limites de controle estreitos e a sobredispersão fazem com que vários subgrupos pareçam fora de controle.
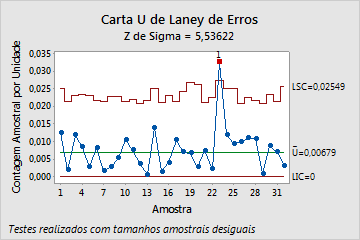
- Carta U' de Laney
- Os limites de controle na carta U' de Laney são ajustados para sobredispersão. A carta U' de Laney mostra que apenas 23 subgrupos estão fora de controle.
Testes para causas especiais
Os testes para causas especiais avaliam se os pontos representados são distribuídos aleatoriamente dentro dos limites de controle.
Interpretação
Use os testes para causas especiais para determinar quais observações você pode precisar investigar e identificar padrões e tendências específicas em seus dados. Cada um dos testes para causas especiais detecta um padrão ou tendência específico em seus dados, o que revela um aspecto diferente da instabilidade do processo. Por exemplo, o Teste 1 detecta um único ponto fora de controle. O Teste 2 detecta uma possível mudança no processo.
Quatro testes estão disponíveis com esta carta de controle.
- Teste 1: um ponto a mais do que 3σ da linha central
- O teste 1 identifica subgrupos que são atípicos se comparados a outros subgrupos. O teste 1 é
reconhecido universalmente como necessário para a detecção de situações fora
de controle. Se pequenas mudanças no processo forem de interesse, você pode
usar o Teste 2 para suplementar o Teste 1, a fim de criar uma carta de
controle que tenha maior sensibilidade.
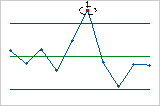
- Teste 2: nove pontos em uma linha no mesmo lado da linha central
- O Teste 2 identifica mudanças na taxa de defeitos do processo. Se pequenas mudanças no processo forem de interesse, você pode usar o Teste 2 para suplementar o Teste 1, a fim de criar uma carta de controle que tenha maior sensibilidade.
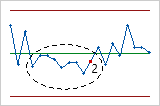
- Teste 3: seis pontos em uma linha, todos crescentes ou todos decrescentes
- O Teste 3 detecta tendências. Este teste procura uma longa série de pontos consecutivos que aumentam consistentemente em valor ou que diminuem em valor.
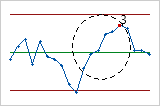
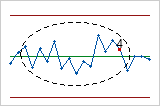
- Teste 4: quatorze pontos em uma linha, alternando para cima e para baixo
- O Teste 4 detecta a variação sistemática. Você deseja que o padrão de variação em um processo seja aleatório, mas um ponto que falha no Teste 4 pode indicar que o padrão de variação é previsível.
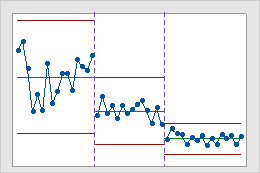
Estágios
Use estágios para criar uma carta de controle histórico, que mostra como um processo muda durante períodos específicos de tempo. Por padrão, o Minitab recalcula a linha central e os limites de controle de cada estágio. Para obter mais informações, acesse Adicionar estágios para exibir mudanças no processo.
Interpretação
Esta carta de controle histórico mostra três estágios de um processo, que representa antes, durante e depois da implementação de um novo procedimento.