Índices de capacidade para dados transformados por Johnson
A transformação de Johnson faz uma seleção ideal de uma função de três famílias de distribuições de uma variável, que são facilmente transformadas em uma distribuição normal padrão. Estas distribuições são rotuladas SB, SL e SU, em que B, L e U referem-se à variável a ser delimitada, lognormal, e ilimitada. O Minitab identifica os parâmetros para as distribuições como primeira forma, segunda forma, localização e escala. Para obter mais informações, acesse Métodos e fórmulas para transformações em Identificação de distribuição individual e clique em "Métodos e fórmulas para a transformação de Johnson".
Quando ambos os limites de especificação estão no intervalo da função de transformação, o Minitab calcula os índices globais com base na capacidade de distribuição normal para os dados transformados. Para obter mais informações, vá para Métodos e fórmulas para medidas globais de capacidade em Análise de capacidade normal.
Quando a família selecionada é o tipo SB ou SL e o limite inferior e/ou superior da especificação está fora do intervalo de distribuição, o Minitab realiza cálculos adicionais para gerar os índices globais de capacidade.
Distribuição SB
Se pelo menos um dos limites de especificação (X) está fora da faixa de distribuição (não ε <X <ε + λ) antes da transformação, Pp, Ppk, PPL, PPU, Z.LSL e Z.USL são calculados como a seguir.
Em primeiro lugar, o Minitab calcula os percentis no espaço transformado.
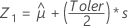
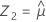
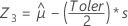
Usando os três valores de Z, Minitab calcula os valores correspondentes de X1, X2 e X3 no espaço original:
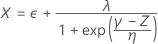
Os índices de capacidade global são então calculados a partir dos valores de X e os valores dos limites de especificação.

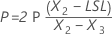

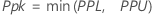


Notação
| Term | Description |
|---|---|
| LSL | Limite inferior de especificação |
| USL | Limite superior de especificação |
 | Media da amostra (X̅) dos dados transformados |
| Toler | Tolerância em desvios padrão |
| s | Desvio padrão da amostra dos dados transformados |
| ε, | Parâmetro de localização da transformação de Johnson |
| Y | Parâmetro de forma da transformação de Johnson |
| η | Parâmetro de forma da transformação de Johnson (η >0) |
| λ | Parâmetro de escala da transformação de Johnson (λ > 0) |
Os cálculos para Z.Bench e os valores de desempenho esperado para uma distribuição SB dependem das localizações de LSV e USL em relação a X2 aos limites de distribuição.
- LSL e USL estão nos lados opostos de X2
-
- Quando LSL e USL estão fora do intervalo de distribuição, o Minitab exibe o seguinte:
Z.Bench está faltando
PPM < LSL = 0
PPM > USL = 0
PPM Total = 0
- Quando um limite de especificação está fora do intervalo de distribuição e outro limite de especificação está dentro do intervalo de distribuição, o Minitab calcula os seguintes valores:

PPM para o limite de especificação fora do intervalo = 0
PPM para o limite de especificação dentro do intervalo = p*1000000
PPM Total = p*1000000
Note
O Minitab usa os dados transformados e os limites de especificação transformados para calcular o PPM.
- Quando LSL e USL estão fora do intervalo de distribuição, o Minitab exibe o seguinte:
- LSL e USL estão à esquerda de X2
-
- Quando LSL e USL estão fora do intervalo de distribuição, o Minitab exibe o seguinte:
Z.Bench está faltando
PPM < LSL = 0
PPM > USL = 1
PPM Total = 1
- Quando LSL está fora do intervalo de distribuição e USL está dentro do intervalo de distribuição, o Minitab calcula os seguintes valores:

PPM < LSL = 0
PPM > USL = p*1000000
PPM Total = PPM > USL
Note
O Minitab usa os dados transformados e os limites de especificação transformados para calcular o PPM.
- Quando LSL e USL estão fora do intervalo de distribuição, o Minitab exibe o seguinte:
- LSL e USL estão à direita de X2
-
- Quando LSL e USL estão fora do intervalo de distribuição, o Minitab exibe o seguinte:
Z.Bench está faltando
PPM < LSL = 1
PPM > USL = 0
PPM Total = 1
- Quando LSL está dentro do intervalo de distribuição e USL está fora do intervalo de distribuição, o Minitab calcula os seguintes valores:

PPM < LSL = p*1000000
PPM > USL = 0
PPM Total = PPM < LSL
Note
O Minitab usa os dados transformados e os limites de especificação transformados para calcular o PPM.
- Quando LSL e USL estão fora do intervalo de distribuição, o Minitab exibe o seguinte:
Distribuição SL
Se pelo menos um dos limites de especificação está fora do intervalo de distribuição antes da transformação, o Minitab usa o mesmo método como mostrado acima para a distribuição de SB para calcular Pp, Ppk, PPL, PPU, Z.LSL e Z.USL. A única mudança é a fórmula para encontrar o valor original de X a partir do valor de Z transformado.

- LSL e USL são menores ou iguais a ε (ambos estão fora do intervalo de distribuição)
-
Z.Bench está faltando
PPM < LSL = 0
PPM > USL = 1
PPM Total = 1
- LSL é menor ou igual a ε
-

PPM < LSL = 0
PPM > USL = p*1000000
PPM Total = PPM > USL
Notação
| Term | Description |
|---|---|
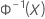 | A função distribuição acumulada (fda) inversa da distribuição normal padrão |
| p | Probabilidade dos dados transformados se estarem fora do limite de especificação transformado |
