Neste tópico
Estimando o desvio padrão
A análise de capacidade entre/dentro baseia-se nos quatro desvios padrão a seguir:
Desvio padrão dentro do subgrupo
σdentro é uma estimativa da variação dentro dos subgrupos (por exemplo, um turno de trabalho, um operador ou de um lote de material). O Minitab estima σdentro utilizando um dos métodos a seguir:
- Desvio padrão combinado:

onde:
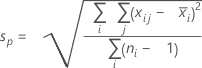
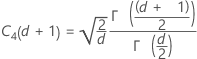
Observação
Se você alterar o método padrão e optar por não usar a constante não viciada, σdentro é estimada por Sp.
Termo Descrição d Graus de liberdade para Sp= Σ (ni- 1) Xij ja observação no io subgrupo X̅i Média do io subgrupo ni Número de observações no io subgrupo C4(d+1) Constante não viciada Γ(·) Função gama - Média dos intervalos do
subgrupo (Rbar):

onde:
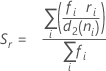
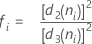
Se n forem todos iguais:
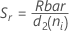
Termo Descrição ri Variação do io subgrupo d2 (ni) Uma constante não viciada obtém dados de uma tabela (para obter mais informações, consulte a seção Constantes não viciadas d2(), d3() e d4() d3 (ni) Uma constante não viciada obtém dados de uma tabela (para obter mais informações, consulte a seção Constantes não viciadas d2(), d3() e d4() ni Número de observações no io subgrupo - A média dos desvios padrão
do subgrupo (Sbar):

onde:
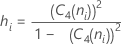
Observação
Se você alterar a configuração padrão e não usar a constante não viciada, σdentro é estimada por Σ Si / número de subgrupos.
Termo Descrição C4(ni) Constante não viciada (conforme definido para o desvio padrão combinado) Si Desvio padrão do subgrupo i ni Número de observações no io subgrupo
Desvio padrão entre subgrupo
σEntre é uma estimativa da variação entre subgrupos (por exemplo, os subgrupos coletados em intervalos definidos, lotes, ou por operadores diferentes).

- Média da amplitude móvel:

onde:

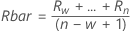
Termo Descrição Ri A iª amplitude móvel w O número de observações utilizadas na amplitude móvel. O padrão é w = 2. d2(w) Uma constante não viciada obtém dados de uma tabela (para obter mais informações, consulte a seção Constantes não viciadas d2(), d3() e d4() - Mediana da amplitude móvel

onde:

Termo Descrição AMi A iª amplitude móvel 
Mediana de AMi w O número de observações utilizadas na amplitude móvel. O padrão é w = 2. d4(w) Uma constante não viciada obtém dados de uma tabela (para obter mais informações, consulte a seção Constantes não viciadas d2(), d3() e d4() - Raiz quadrada das diferenças
sucessivas do quadrado médio (MSSD):
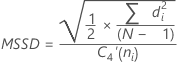
Observação
Se você alterar a configuração padrão e não usar a constante não viciada, σdentro é estimado por

Termo Descrição di Diferenças de médias do grupo sucessivas C4(ni) Constante não viciada (conforme definido para o desvio padrão combinado) C4'(ni) Constante não viciada ≈ c4(ni). Para obter mais informações, consulte a seção Constantes não viciadas c4(). N Número de observações total ni Número de observações no io subgrupo
Desvio padrão entre/dentro

| Termo | Descrição |
|---|---|
| σ2Entre | Variância entre subgrupos |
| σ2entre | Variância dentro de subgrupos |
Desvio padrão global

onde:
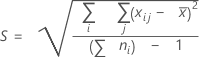
Observação
Por padrão, o Minitab não usa a constante não viciada ao estimar σglobal. σglobal é estimado por S. Se você quer estimar o desvio padrão total usando a constante não viciada, você pode mudar esta opção na subcaixa de diálogo Estimativa quando você realizar a análise de capacidade. Se você quiser que sempre o Minitab use a constante não viciada por padrão, escolha e selecione as opções apropriadas.
| Termo | Descrição |
|---|---|
| Xij | A ja observação no io subgrupo |
| X̅ | Média do processo |
| ni | Número de observações no io subgrupo |
| C4 (N) | Constante não viciada (conforme definido para o desvio padrão combinado) |
| N (ou, Σ ni) | Número de observações total |
Transformação Box-Cox
A transformação de Box-Cox calcula um valor de lambda, como mostrado na tabela a seguir, o que minimiza o desvio padrão de uma variável de transformada padronizada. A transformação resultante é Yλ quando λ ҂ 0 e In Y quando λ = 0.
O método Box-Cox pesquisa através de muitos tipos de transformações. A tabela a seguir mostra algumas transformações comuns onde Y' é a transformação do Y dos dados.
| Valor lambda (λ) | Transformação |
|---|---|
 |
 |
 |
 |
 |
 |
 |
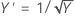 |
 |
 |
