Neste tópico
Carta U
Uma carta U representa graficamente o número de defeitos (também chamadas de não-conformidades) por unidade. A linha central é o número médio de defeituosos por unidade (ou subgrupo). Os limites de controle, que são fixados a uma distância de 3 desvios padrão acima e abaixo da linha central, mostram a quantidade de variação esperada nas médias do subgrupo.
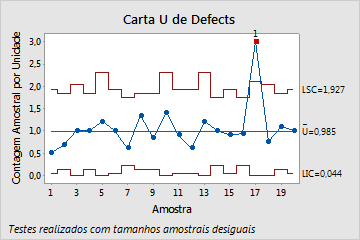
Esta carta U mostra que, em média, a taxa de defeitos por unidade nas amostras é de aproximadamente 1. Um ponto aparece fora de controle.
Interpretação
Use a carta U para monitorar visualmente os defeitos por unidade e para determinar se a taxa de defeitos está estável e sob controle.
Os pontos vermelhos indicam subgrupos que falharam em pelo menos um dos testes para causas especiais e não estão sob controle. Pontos fora de controle indicam que o processo pode não estar estável e que os resultados de uma análise de capacidade pode não ser confiável. Você deve identificar a causa de pontos fora de controle e eliminar as variações de causas especiais antes de analisar a capacidade do processo.
Testes para causas especiais
Os testes para causas especiais avaliam se os pontos obtidos em cada carta de controle são distribuídos aleatoriamente dentro dos limites de controle.
Interpretação
Use os testes para causas especiais para determinar quais observações você pode precisar investigar e identificar padrões e tendências específicas em seus dados. Cada um dos testes para causas especiais detecta um padrão ou tendência específica em seus dados, o que revela um aspecto diferente da instabilidade do processo.
- Um ponto a mais que 3 sigmas da linha central
- O teste 1 identifica os subgrupos que são incomuns em comparação com outros subgrupos. O
teste 1 é reconhecido universalmente como necessário para a detecção de
situações fora de controle. Se pequenas mudanças no processo forem de
interesse, você pode usar o Teste 2 para suplementar o Teste 1 a fim de
criar uma carta de controle que tenha maior sensibilidade.
- Nove pontos consecutivos do mesmo lado da linha central
- O Teste 2 identifica mudanças na variação do processo. Se pequenas mudanças no processo
forem de interesse, você pode usar o Teste 2 para suplementar o Teste 1
a fim de criar uma carta de controle que tenha maior sensibilidade.
- Seis pontos consecutivos, todos crescentes ou decrescentes
- O teste 3 detecta tendências. Este teste procura uma longa série de pontos consecutivos que
aumentam consistentemente em valor ou que diminuem em valor.
- Quatorze pontos consecutivos, alternando para cima e baixo
- O teste 4 detecta variação sistemática. Você deseja que o padrão de variação em um processo
seja aleatório, mas um ponto que falha no Teste 4 pode indicar que o
padrão de variação é previsível.
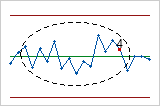
Gráfico de DPU acumulado
Os pontos do gráfico de DPU acumulado mostram a média DPU para cada amostra. Os pontos são exibidas na ordem em que as amostras foram coletadas. A linha horizontal do meio representa a média de DPU calculada a partir de todas as amostras. As linhas horizontais superiores e inferiores representam os limites de confiança superior e inferior para a média de DPU.
Interpretação
Use o Gráfico de %Defeituosos acumulado para ajudá-lo a determinar se você coletou amostras suficientes para ter uma estimativa estável do DPU.
Examine os defeitos por unidade para as amostras ordenadas por horário para ver como a estimativa muda conforme você coleta mais amostras. De maneira ideal, o DPU deve estabilizar depois de várias amostras, como mostrado por um achatamento dos pontos representados graficamente ao longo da linha de DPU.
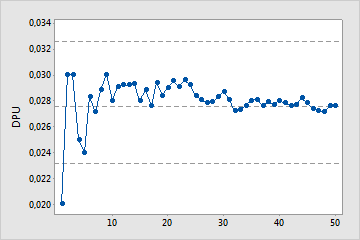
Amostras suficientes
Este estudo de capacidade inclui amostras suficientes para estimar os defeitos médios por unidade.
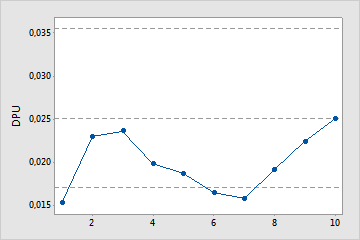
Sem amostras suficientes
Este estudo de capacidade não inclui amostras suficientes para estimar os defeitos médios por unidade.
Gráfico de Poisson
O gráfico de Poisson apresenta o número observado de defeitos em relação ao número esperado de defeitos. A linha diagonal mostra onde os dados cairiam se ele seguissem perfeitamente a distribuição de Poisson. Se os dados se desviarem significativamente a partir desta linha, a análise de capacidade de Poisson não pode fornecer resultados confiáveis.
Observação
O Minitab exibe um gráfico de Poisson quando os tamanhos dos subgrupos são iguais. Se os tamanhos de subgrupos variarem, o Minitab exibe um gráfico de taxa de defeitos. Para obter mais informações, consulte a seção sobre o Gráfico de taxa de defeitos .
Interpretação
Use o gráfico de Poisson para avaliar se seus dados seguem a distribuição de Poisson.
Examine o gráfico para determinar se os pontos representados graficamente seguem aproximadamente uma linha reta. Se não, o pressuposto de que os dados foram amostrados a partir de uma distribuição de Poisson pode ser falso.
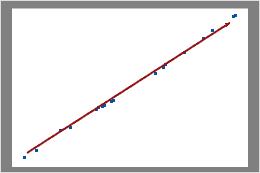
Nestes resultados, os pontos de dados enquadram-se muito proximamente ao longo da linha. Você pode assumir que os dados seguem uma distribuição de Poisson.
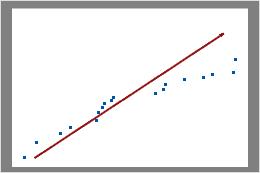
Considerando tais resultados, os pontos de dados não caem ao longo da linha perto da parte superior direita do gráfico. Esses dados não seguem uma distribuição de Poisson e não podem ser avaliados de forma confiável usando a análise de capacidade Poisson.
Gráfico de taxa de defeitos
O gráfico de taxa de defeitos mostra o número de defeitos por unidade (DPU) em cada subgrupo e o tamanho de cada subgrupo. A linha central é igual ao DPU médio.
Observação
O Minitab exibe um Gráfico de taxa de defeitos quando os tamanhos de subgrupos variarem. Se os tamanhos dos subgrupos forem constantes, o Minitab exibe um gráfico de Poisson. Para obter mais informações, consulte a seção sobre o gráfico de Poisson.
Interpretação
Use o Gráfico de taxa de defeitos para verificar se os seus dados são de Poisson, verificando a hipótese de que o número de defeitos por unidade é constante entre os diferentes tamanhos de amostra.
Examine o gráfico para avaliar se os defeitos por unidade (DPU) são distribuídos aleatoriamente em tamanhos de amostra ou se um padrão está presente. Se os seus dados caírem aleatoriamente sobre a linha central, conclua que os dados seguem uma distribuição de Poisson.
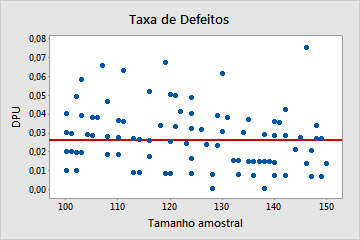
Poisson
Neste gráfico, os pontos são dispersos aleatoriamente ao redor da linha central. Você pode assumir que os dados seguem uma distribuição de Poisson.
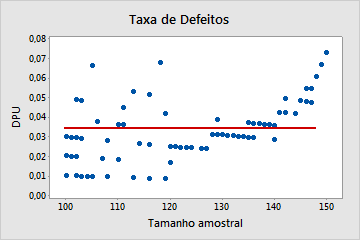
Não Poisson
Neste gráfico, o padrão não é aleatório. Para o tamanho de amostra maior que 120, o DPU aumenta conforme o tamanho da amostra aumenta. Este resultado sugere uma possível correlação entre o tamanho da amostra e a taxa de defeitos. Portanto, os dados não seguem uma distribuição de Poisson e não podem ser avaliados de forma confiável usando a análise de capacidade Poisson.
Histograma
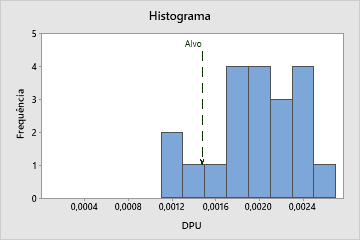
Interpretação
Use a distribuição do histograma de DPU para avaliar a distribuição dos defeitos por unidade de medida em suas amostras.
Examine o pico e a dispersão da distribuição dos defeitos por unidade. O pico representa os valores mais comuns e aproxima-se do centro dos defeitos por unidade. Avalie a dispersão para entender o quanto defeitos por unidade varia entre as amostras.
Compare a linha de referência para o valor alvo com as barras do histograma. Se o processo for capaz, a maioria ou todas as barras do histograma deve estar à esquerda do valor alvo.
DPU médio
Os defeitos médios por unidade (DPU) são a média dos defeitos por unidade de medida através das amostras.
Interpretação
Use o DPU médio para estimar o número médio de defeitos que você pode esperar para cada unidade e para determinar se o seu processo atende às expectativas dos clientes.
Compare o DPU médio com a DPU alvo para ver se o processo atende aos requisitos. Se o DPU médio for maior do que o alvo, você deve aprimorar seu processo.
Você também deve comparar o alvo com o IC superior para DPU. Se o IC superior for maior do que o alvo, não é possível ter certeza que DPU médio para seu processo seja menor que o alvo. Talvez seja necessário um tamanho amostral maior para determinar com mais confiança se o processo está no alvo.
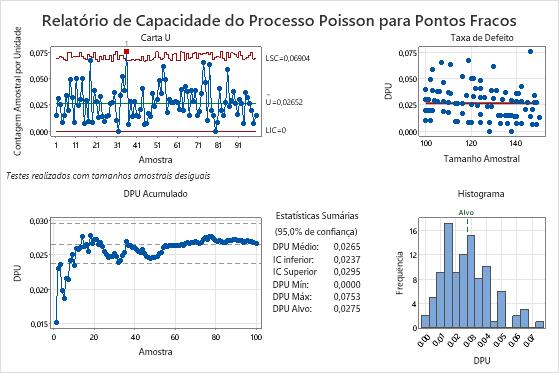
Por exemplo, na tabela de Estatísticas de Resumo da saída a seguir, a DPU média (0,0265) é menor do que o alvo (0,0275). No entanto, o IC superior é 0,0295, que é maior do que o alvo. Embora o processo atenda aos requisitos, uma amostra maior é necessária para determinar com mais certeza se o DPU está abaixo da meta.
Intervalo de confiança (IC)
O intervalo de confiança é um intervalo de valores prováveis para um índice de capacidade. O intervalo de confiança é definido por um limite inferior e um limite superior. Os limites são calculados determinando-se uma margem de erro para a estimativa da amostra. O limite inferior de confiança define um valor deve ser menor ou igual ao índice de capacidade. O limite superior de confiança define um valor que deve ser maior ou igual ao índice de capacidade.
O Minitab exibe tanto um limite de confiança inferior como um limite de confiança superior para a média DPU.
Interpretação
Como as amostras de dados são aleatórias, é improvável que as diferentes amostras coletadas em seu processo produzam estimativas idênticas de um índice de capacidade. Para calcular o valor real do índice de capacidade para o seu processo, você precisa analisar os dados para todos os itens que o processo produz, o que não é viável. Em vez disso, você pode usar um intervalo de confiança para determinar um intervalo de valores prováveis para o índice de capacidade.
A um nível de confiança de 95%, é possível ter 95% de confiança de que o valor real do índice de capacidade esteja contido dentro do intervalo de confiança. Ou seja, se você coletar 100 amostras aleatórias de seu processo, você pode esperar que cerca de 95 das amostras produzam intervalos que contêm o valor real do índice de capacidade.
O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Quando possível, compare os limites de confiança a um valor de benchmark que esteja baseado em padrões de conhecimento de processo ou do setor.
Por exemplo, o máximo admissível de defeitos médios por unidade para um processo de fabricação é de 0,025%. Com a análise de capacidade de Poisson, os analistas obtêm uma estimativa do DPU médio de 0,011%, o que sugere que o processo é capaz. No entanto, o IC superior para o DPU médio é 0,029%. Portanto, os analistas não podem ter a confiança de 95% de que o DPU médio da população não vá exceder o valor máximo admissível. Talvez seja necessário usar uma amostra maior ou reduzir a variabilidade dos dados para obter um intervalo de confiança mais estreito para a estimativa da amostra.
DPU mínimo
O DPU mín são os defeitos mínimos por unidade de medição entre todas as amostras.
Interpretação
Use o DPU mínimo para estimar o número mínimo de defeitos que você pode esperar para cada unidade.
DPU máximo
O DPU máx são os defeitos máximos por unidade de medição entre todas as amostras.
Interpretação
Use o DPU máximo para estimar o número máximo de defeitos que você pode esperar para cada unidade.
DPU alvo
O DPU alvo é o número máximo de defeitos por unidade que você está disposto a aceitar. Se você não especificar um DPU alvo, o Minitab assume um alvo de 0 para DPU.
Interpretação
Compare o DPU médio com a DPU alvo para ver se o processo atende aos requisitos. Se o DPU médio for maior do que o alvo, você deve aprimorar seu processo.
Você também deve comparar o alvo com o IC superior para DPU. Se o IC superior for maior do que o alvo, não é possível ter certeza que DPU médio para seu processo seja menor que o alvo. Talvez seja necessário um tamanho amostral maior para determinar com mais confiança se o processo está no alvo.

Por exemplo, na tabela de Estatísticas de Resumo, a DPU média (0,0265) é menor do que o alvo (0,0275). No entanto, o IC superior para DPU é 0,0295, que é maior do que o alvo. Embora o processo pareça atender aos requisitos, você precisa de um tamanho amostral maior para confirmar com maior confiança se o DPU está abaixo da meta.
